题目内容
已知a＝2e1－3e2，b＝2e1＋3e2，其中e1，e2不共线，向量c＝2e1－9e2，那么是否存在这样的实数λ，μ，使d＝λa＋μb与c共线？
解析：存在，由已知得，
d＝λa＋μb
＝λ(2e1－3e2)＋μ(2e1＋3e2)＝2(λ＋μ)e1＋3(μ－λ)e2，
若d与c共线，则存在实数m，使d＝mc，即2(λ＋μ)e1＋3(μ－λ)e2＝m(2e1－9e2)，
得2(λ＋μ－m)e1＝3(λ－μ－3m)e2，
因为e1，e2不共线，所以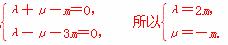
得λ＝－2μ，所以存在这样的实数λ，μ满足λ＝－2μ，使d＝λa＋μb与c共线．
练习册系列答案
相关题目
，求S△AOB.
(φ为参数)的右焦点，且与直线
(t为参数)平行的直线的普通方程．
线段OD的中点，AE的延长线与CD交于点F.若
＝a，
＝b，则
＝( )
a＋
b B.
a＋
b
，则λ＝________.
k)共线且方向相反，则k＝( )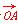
＝(3,4)，
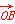＝(6，－3)，
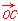＝(5－m，－3－m)．若点A，B，C能构成三角形，求实数m满足的条件．
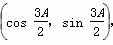，n＝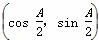
，且满足|m＋n|＝
.
|＋|
|＝
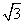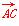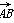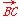|，试判断△ABC的形状．