题目内容
如图，正方体ABCD－A1B1C1D1中，E、F分别是AB和AA1的中点．求证：
(1)E、C、D1、F四点共面；
(2)CE、D1F、DA三线共点．
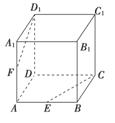
证明：(1)如图，连接EF，CD1，A1B.
∵E、F分别是AB、AA1的中点，
∴EF∥BA1.
又A1B∥D1C，
∴EF∥CD1，
∴E、C、D1、F四点共面．
(2)∵EF∥CD1，EF＜CD1，
∴CE与D1F必相交，设交点为P，则由P∈CE，CE⊂平面ABCD，
得P∈平面ABCD.
同理P∈平面ADD1A1.
又平面ABCD∩平面ADD1A1＝DA.
∴P∈直线DA，∴CE、D1F、DA三线共点．
练习册系列答案
相关题目
(x>0)，观察：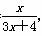
，
，
，
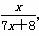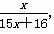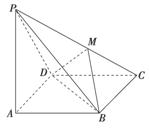
，那么当该棱锥的体积最大时，它的高为( )
C．2 D．3
直线有________条．
＝
，则直线MN与平面BDC的位置关系是__________．
都相等，M是PC上的一动点，当点M满足__________时，平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可) 