题目内容
四棱锥P—ABCD中,底面ABCD是矩形,PA 底面ABCD,PA=" AB" =1,AD =2,点M是PB的中点,点N在BC边上移动.
底面ABCD,PA=" AB" =1,AD =2,点M是PB的中点,点N在BC边上移动.
(I)求证:当N是BC边的中点时,MN∥平面PAC;
(Ⅱ)证明,无论N点在BC边上何处,都有PN AM;
AM;
(Ⅲ)当BN等于何值时,PA与平面PDN所成角的大小为45 .
.
 底面ABCD,PA=" AB" =1,AD =2,点M是PB的中点,点N在BC边上移动.
底面ABCD,PA=" AB" =1,AD =2,点M是PB的中点,点N在BC边上移动.(I)求证:当N是BC边的中点时,MN∥平面PAC;
(Ⅱ)证明,无论N点在BC边上何处,都有PN
 AM;
AM;(Ⅲ)当BN等于何值时,PA与平面PDN所成角的大小为45
 .
.
(Ⅰ)取 的中点
的中点 ,连接
,连接 ,又因为
,又因为 是
是 的中点,
的中点, 是
是 中点.
中点.
 ∥
∥ ,
, ∥
∥ .
.
 ,
,
 ,
,
 平面
平面 ∥平面
∥平面 .又
.又 平面
平面 ,
,
 ∥平面
∥平面 ………………4分
………………4分

(Ⅱ) ,
, 是
是 的中点,
的中点, .
.
又 平面
平面 ,
, 平面
平面 ,
, .
.
又 ,
, ,
, 平面
平面 .
.
又 平面
平面 ,
, .
. 平面
平面 .
.
又 平面
平面 ,
,
 .
.
所以无论 点在
点在 边的何处,都有
边的何处,都有 .
.
(Ⅲ)分别以 所在的直线为
所在的直线为 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设

则 ,
, ,
, ,
, ,
,
 ,
, ,
, ,
,
 ,
, 设平面
设平面
 的法向量为
的法向量为 ,则
,则


令 得
得 ,
, ,
,
设 与平面
与平面 所成的角为
所成的角为 ,
,

 ,
,
 ,解得
,解得 或
或 (舍去).
(舍去). 
 的中点
的中点 ,连接
,连接 ,又因为
,又因为 是
是 的中点,
的中点, 是
是 中点.
中点. ∥
∥ ,
, ∥
∥ .
.
 ,
,
 ,
, 平面
平面 ∥平面
∥平面 .又
.又 平面
平面 ,
,
 ∥平面
∥平面 ………………4分
………………4分 
(Ⅱ)
 ,
, 是
是 的中点,
的中点, .
.又
 平面
平面 ,
, 平面
平面 ,
, .
.又
 ,
, ,
, 平面
平面 .
.又
 平面
平面 ,
, .
. 平面
平面 .
.又
 平面
平面 ,
,
 .
.所以无论
 点在
点在 边的何处,都有
边的何处,都有 .
.(Ⅲ)分别以
 所在的直线为
所在的直线为 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设

则
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, 设平面
设平面 的法向量为
的法向量为 ,则
,则

令
 得
得 ,
, ,
,设
 与平面
与平面 所成的角为
所成的角为 ,
,
 ,
, ,解得
,解得 或
或 (舍去).
(舍去). 
略

练习册系列答案
相关题目


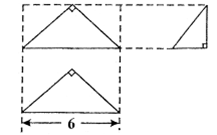





 的等边三角形,则该圆锥的表面积为【 】.
的等边三角形,则该圆锥的表面积为【 】.



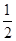 a2
a2 a2
a2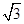 a2
a2
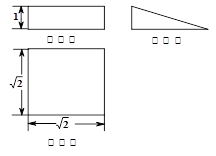
 ,当圆柱的半径R等于( )时,所用的材料最省(表面积最小).
,当圆柱的半径R等于( )时,所用的材料最省(表面积最小).