题目内容
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60o(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4 km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
(1)将tanq表示为x的函数;
(2)求点D的位置,使q取得最大值.

 km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.(1)将tanq表示为x的函数;
(2)求点D的位置,使q取得最大值.

(1) ;(2)
;(2)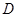 点距
点距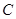 点6km.
点6km.
 ;(2)
;(2)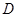 点距
点距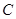 点6km.
点6km.试题分析:(1)由图可知
 ,因此为了求
,因此为了求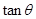 ,可通过求
,可通过求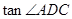 和
和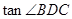 ,
,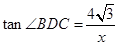 ,下面关键要求
,下面关键要求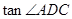 ,为止作
,为止作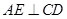 ,垂足为
,垂足为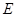 ,这时会发现随
,这时会发现随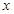 的取值不同,
的取值不同,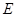 点可能在线段
点可能在线段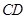 上,也可能在线段
上,也可能在线段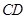 外,
外,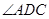 可能为锐角也可能为钝角,这里出现了分类讨论,作
可能为锐角也可能为钝角,这里出现了分类讨论,作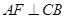 交
交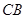 延长线于
延长线于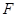 ,由已知可求出
,由已知可求出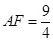 ,这就是分类的分界点;(2)由(1)求得
,这就是分类的分界点;(2)由(1)求得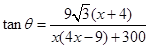 ,要求它的最大值,可以采取两种方法,一种是由于分子是一次,分母是二次的,可把分子
,要求它的最大值,可以采取两种方法,一种是由于分子是一次,分母是二次的,可把分子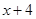 作为整体,分子分母同时除以
作为整体,分子分母同时除以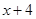 (当然分母也已经化为
(当然分母也已经化为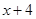 的多项式了),再用基本不等式求解,也可用导数知识求得最大值.
的多项式了),再用基本不等式求解,也可用导数知识求得最大值.(1)过A分别作直线CD,BC的垂线,垂足分别为E,F.
由题知,AB=4.5,BC=4
 ,∠ABF=90o-60o=30o,
,∠ABF=90o-60o=30o,所以CE=AF=4.5×sin30o=
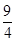 ,BF=4.5×cos30o=
,BF=4.5×cos30o= ,
,AE=CF=BC+BF=

 .
.因为CD=x(x>0),所以tan∠BDC=
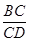 =
=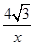 .
.当x>
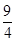 时,ED=x-
时,ED=x-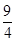 ,tan∠ADC=
,tan∠ADC=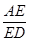 =
=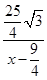 =
=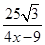 (如图1);
(如图1);
当0<x<
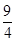 时,ED=
时,ED=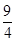 -x,tan∠ADC=-
-x,tan∠ADC=-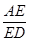 =
=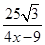 (如图2). 4分
(如图2). 4分所以tanq=tan∠ADB=tan(∠ADC-∠BDC)=
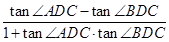
=
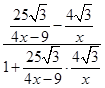 =
=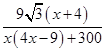 ,其中x>0且x≠
,其中x>0且x≠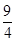 .
. 当x=
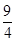 时tanq=
时tanq=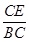 =
=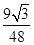 ,符合上式.
,符合上式.所以tanq=
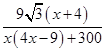 ( x>0) 8分
( x>0) 8分(2)(方法一)tanq==
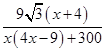 =
= ,x>0. 11分
,x>0. 11分因为4(x+4)+
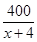 -41≥2
-41≥2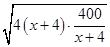 -41=39,
-41=39,当且仅当4(x+4)=
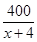 ,即x=6时取等号.
,即x=6时取等号.所以当x=6时,4(x+4)+
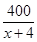 -41取最小值39.
-41取最小值39.所以当x=6时,tanq取最大值
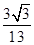 . 13分
. 13分由于y=tanx在区间(0,
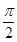 )上是增函数,所以当x=6时,q取最大值.
)上是增函数,所以当x=6时,q取最大值.答:在海湾一侧的海岸线CT上距C点6km处的D点处观看飞机跑道的视角最大 14分
(方法二)tanq=f(x)=
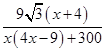 =
=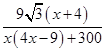 .
.f ¢(x)=
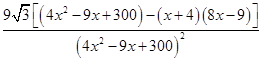 =-
=-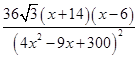 ,x>0.
,x>0.由f ¢(x)=0得x=6. 11分
当x∈(0,6)时,f ¢(x)>0,函数f(x)单调递增;当x∈(6,+∞)时,f ¢(x)<0,此时函数f(x)单调递减.
所以函数f(x)在x=6时取得极大值,也是最大值f(6)=
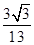 . 13分
. 13分由于y=tanx在区间(0,
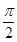 )上是增函数,所以当x=6时,q取最大值.
)上是增函数,所以当x=6时,q取最大值.答:在海湾一侧的海岸线CT上距C点6km处的D点处观看飞机跑道的视角最大. 14分

练习册系列答案
相关题目
 ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π. ,求f(θ)的值;
,求f(θ)的值; 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
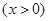 ,其中
,其中 ,
, 为正整数,
为正整数,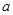 ,
, ,
, 均为常数,曲线
均为常数,曲线 在
在 处的切线方程为
处的切线方程为 .
. 的最大值;
的最大值; 都有
都有 .(
.( 为自然对数的底)
为自然对数的底)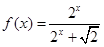 .
.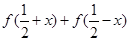 的值;
的值;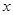 的不等式:
的不等式: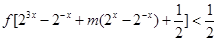 在区间
在区间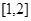 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.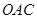 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域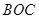 内,乙中转站建在区域
内,乙中转站建在区域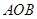 内.分界线
内.分界线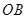 固定,且
固定,且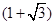 百米,边界线
百米,边界线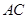 始终过点
始终过点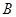 ,边界线
,边界线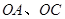 满足
满足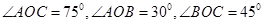 .
.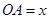 (
(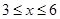 )百米,
)百米,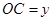 百米.
百米.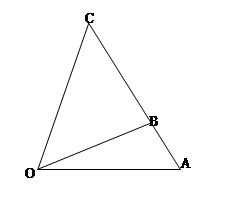
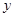 表示成
表示成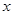 的函数,并求出函数
的函数,并求出函数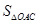 最小,并求出其面积的最小值.
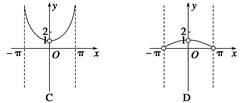
最小,并求出其面积的最小值.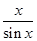 ,x∈(-π,0)∪(0,π)的图象可能是下列图象中的( )
,x∈(-π,0)∪(0,π)的图象可能是下列图象中的( )
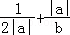 取得最小值.
取得最小值. 与函数
与函数 的图像分别交于点
的图像分别交于点 ,则当
,则当 达到最小时
达到最小时 的值为( )
的值为( )


 的单调递减区间是________________.
的单调递减区间是________________.