题目内容
(12分)(2011•福建)设函数f(θ)= ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(Ⅰ)若点P的坐标为 ,求f(θ)的值;
,求f(θ)的值;
(Ⅱ)若点P(x,y)为平面区域Ω: 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
 ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.(Ⅰ)若点P的坐标为
 ,求f(θ)的值;
,求f(θ)的值;(Ⅱ)若点P(x,y)为平面区域Ω:
 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.(Ⅰ)2(Ⅱ) 时,f(θ)取得最大值2;θ=0时,f(θ)取得最小值1
时,f(θ)取得最大值2;θ=0时,f(θ)取得最小值1
 时,f(θ)取得最大值2;θ=0时,f(θ)取得最小值1
时,f(θ)取得最大值2;θ=0时,f(θ)取得最小值1试题分析:(I)由已知中函数f(θ)=
 ,我们将点P的坐标
,我们将点P的坐标 代入函数解析式,即可求出结果.
代入函数解析式,即可求出结果.(II)画出满足约束条件
 的平面区域,数形结合易判断出θ角的取值范围,结合正弦型函数的性质我们即可求出函数f(θ)的最小值和最大值.
的平面区域,数形结合易判断出θ角的取值范围,结合正弦型函数的性质我们即可求出函数f(θ)的最小值和最大值.解(I)由点P的坐标和三角函数的定义可得:

于是f(θ)=
 =
= =2
=2(II)作出平面区域Ω(即感触区域ABC)如图所示
其中A(1,0),B(1,1),C(0,1)
于是0≤θ≤

∴f(θ)=
 =
=
且

故当
 ,即
,即 时,f(θ)取得最大值2
时,f(θ)取得最大值2当
 ,即θ=0时,f(θ)取得最小值1
,即θ=0时,f(θ)取得最小值1
点评:本题主要考查三角函数、不等式等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件: ,总有
,总有 ;(2)
;(2) ;(3) 若
;(3) 若 ,
, ,且
,且 ,则有
,则有 成立,则称
成立,则称 的值;
的值;  在区间
在区间 ,使得
,使得 且
且 , 求证:
, 求证: .
. (千辆/时)与汽车的平均速度
(千辆/时)与汽车的平均速度 (千米/时)之间的函数关系为
(千米/时)之间的函数关系为 (
( ).
). 千辆/时,则汽车的平均速度应在什么范围内?
千辆/时,则汽车的平均速度应在什么范围内? ,g(x)=x-ln x,若对任意的x1,x2∈[1,e],都有f(x1)≥g(x2)成立,则实数a的取值范围为________.
,g(x)=x-ln x,若对任意的x1,x2∈[1,e],都有f(x1)≥g(x2)成立,则实数a的取值范围为________. log2x,则f(2)=________.
log2x,则f(2)=________.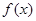 定义在
定义在 上,对任意的
上,对任意的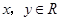 ,
,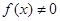 ,且
,且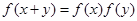 .
.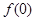 ,并证明:
,并证明: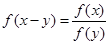 ;
;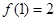 .设向量
.设向量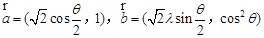 ,对任意
,对任意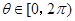 ,
,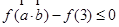 恒成立,求实数
恒成立,求实数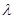 的取值范围.
的取值范围. .
. ,
, 时,若不等式
时,若不等式 恒成立,求
恒成立,求 的范围;
的范围; 在
在 内零点的个数,并说明理由.
内零点的个数,并说明理由. km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.