题目内容
已知四棱锥S--ABCD的底面ABCD是正方形,SA![]() 底面ABCD,点E是SC上任意一点.
底面ABCD,点E是SC上任意一点.

(Ⅰ)求证:平面EBD![]() 平面SAC;
平面SAC;
(Ⅱ)设SA=4,AB=2,求点A到平面SBD的距离;
(Ⅲ)当![]() 的值为多少时,二面角B-SC-D的大小为120°。
的值为多少时,二面角B-SC-D的大小为120°。
证明(Ⅰ):∵ABCD是正方形,∴BD⊥AC,
∵SA⊥底面ABCD,BD![]() 面ABCD,∴SA⊥BD,
面ABCD,∴SA⊥BD,
∵SA![]() AC=A,∴BD⊥面SAC,
AC=A,∴BD⊥面SAC,
又∵BD![]() 面EBD,∴平面EBD⊥平面SAC
面EBD,∴平面EBD⊥平面SAC
解(Ⅱ):由(Ⅰ)知,BD^面SAC,
又∵BDÌ面SBD,∴平面SBD![]() 平面SAC,
平面SAC,
设AC![]() BD=O,
BD=O,
则平面SBD![]() 平面SAC=SO,过A作AF^SO交SO于点F,则AF^面SBD,
平面SAC=SO,过A作AF^SO交SO于点F,则AF^面SBD,
所以线段AF的长就是点A到平面SBD的距离.

∵ABCD是正方形,AB=2,∴AO=![]() ,
,
又∵SA=4,△SAO是Rt△,∴SO=![]() ,
,
∵SO×AF=SA×AO,∴AF=![]() ,∴点A到平面SBD的距离为
,∴点A到平面SBD的距离为![]()
解(Ⅲ):作BM⊥SC于M,连结DM,
∵SA![]() 底面ABCD,AB=AD,∴SB=SD,
底面ABCD,AB=AD,∴SB=SD,
又∵CB⊥AB,CD⊥AD,∴CB⊥SB,CD⊥SD,
∴△SBC≌△SDC,∴DM⊥SC,
∴∠BMD是二面角B-SC-D的平面角,BM=DM
要使∠BMD=120°,只须![]() ,
,
即BM2=![]() ,而BD2=2AB2,∴BM2=
,而BD2=2AB2,∴BM2=![]() AB2,
AB2,
∵BM×SC=SB×BC,SC2=SB2+BC2,
∴BM2×SC2=SB2×BC2,∴![]() AB2(SB2+BC2)= SB2×BC2,
AB2(SB2+BC2)= SB2×BC2,
∵AB=BC,∴2SB2+2AB2=3SB2,∴SB2=2AB2,
又∵AB2=SB2-SA2,∴AB2=SA2,∴![]() ,
,
故当![]() 时,二面角B-SC-D的大小为120
时,二面角B-SC-D的大小为120![]()
解法二:
证明(Ⅰ)同解法一
∵ABCD是正方形,SA![]() 底面ABCD,
底面ABCD,
∴SA⊥AB,SA⊥AD,AB⊥AD,
如图,建立直解坐标系A-xyz.

(Ⅱ)A(0,0,0),B(2,0,0),D(0,2,0),S(0,0,4),
设平面SBD的法向量为![]() ,则
,则![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,
∴![]() ,
,![]() ,而
,而![]() =(2,0,-4),
=(2,0,-4),![]() =(0,2,-4)
=(0,2,-4)
∴![]() ,∴x=2,y=2,即
,∴x=2,y=2,即![]() ,
,
则点A到平面SBD的距离d=![]() =
=![]()
(Ⅲ)设AB=a,SA=b,则A(0,0,0),B(a,0,0),C(a,a,0),D(0,a,0),S(0,0,b),SB=![]() ;
;
设平面SBC的法向量![]() =(x1,y1,-1),平面SDC的法向量
=(x1,y1,-1),平面SDC的法向量![]() =(x2,y2,1)
=(x2,y2,1)
则 ,而
,而![]() =(0,a,0),
=(0,a,0),![]() =(-a,0,0),
=(-a,0,0),![]() =(a,a,-b)
=(a,a,-b)
∴ ,
,
∴x1=![]() ,y1=0,x2=0,y2=
,y1=0,x2=0,y2=![]()
∴![]() =(
=(![]() ,0,-1),
,0,-1),![]() =(0,
=(0, ![]() ,1),
,1),
∴cos<![]() ,
,![]() >=
>=![]() =
=![]() ,
,
要使二面角B-SC-D的大小为120![]() ,
,
只需![]() =-
=-![]() ,即a=b,∴
,即a=b,∴![]() ,
,
故当![]() 时,二面角B-SC-D的大小为120
时,二面角B-SC-D的大小为120![]()

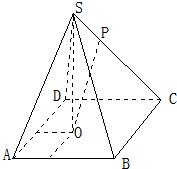 如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,且O到AB、AD的距离分别为2和1. P是SC上的点,
如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,且O到AB、AD的距离分别为2和1. P是SC上的点,
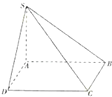 (2011•许昌三模)已知四棱锥S-ABCD中,AB=BC=CD=DA=SA=2,底面ABCD是正方形,SD=SB=
(2011•许昌三模)已知四棱锥S-ABCD中,AB=BC=CD=DA=SA=2,底面ABCD是正方形,SD=SB=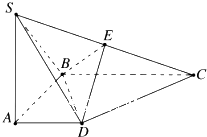 已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=