题目内容
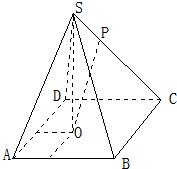如图，已知四棱锥S-ABCD的底面是边长为4的正方形，S在底面上的射影O落在正方形ABCD内，且O到AB、AD的距离分别为2和1． P是SC上的点，| SP |
| PC |
| 1 |
| 3 |
（1）求证：OP∥平面SAD；
（2）求证：
| AB |
| SC |
分析：（1）已知四棱锥S-ABCD的底面是边长为4的正方形，在SD上取一点Q，使
=
，只要证明四边形PQMO是平行四边形，再利用直线与平面平行的判定定理进行证明，即可解决问题；
（2）设点O向BC所引的垂线段为ON，利用向量的乘法进行证明．
| SQ |
| QD |
| 1 |
| 3 |
（2）设点O向BC所引的垂线段为ON，利用向量的乘法进行证明．
解答：解：（1）证明：在SD上取一点Q，使
=
，
设点O向AD所引的垂线段为OM．则OM=1．连接PQ，QM．
∵
=
=
，
∴PQ∥CD．∵OM∥CD，∴PQ∥OM．∵
=
，
∴PQ=1．∴四边形PQMO是平行四边形．
∴OP∥QM，∵QM?平面SAD，PO?平面SAD，
∴OP∥平面SAD．
（2）设点O向BC所引的垂线段为ON．
则ON=3，
∴
•
=
•(
-
)=
•
-
•
=
•
=|
||
|cos∠CON=|
||
|=12．
∴
•
是定值．
| SQ |
| QD |
| 1 |
| 3 |
设点O向AD所引的垂线段为OM．则OM=1．连接PQ，QM．
∵
| SQ |
| QD |
| SP |
| PC |
| 1 |
| 3 |
∴PQ∥CD．∵OM∥CD，∴PQ∥OM．∵
| PQ |
| CD |
| 1 |
| 4 |
∴PQ=1．∴四边形PQMO是平行四边形．
∴OP∥QM，∵QM?平面SAD，PO?平面SAD，
∴OP∥平面SAD．
（2）设点O向BC所引的垂线段为ON．
则ON=3，
∴
| AB |
| SC |
| AB |
| OC |
| OS |
| AB |
| OC |
| AB |
| OS |
| AB |
| OC |
=|
| AB |
| OC |
| AB |
| ON |
∴
| AB |
| SC |
点评：此题考查直线与平面平行的判断及向量的应用，第一问此类问题一般先证明两个面平行，再证直线和面平行，这种做题思想要记住，此类立体几何题是每年高考必考的一道大题，要注意这方面的题．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知四棱锥S-ABCD的底面ABCD是边长为1的正方形，SA⊥平面ABCD，SA=2，E是侧棱SC上的一点．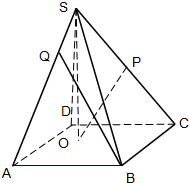
如图，已知四棱锥S-ABCD的底面是边长为4的正方形，S在底面上的射影O落在正方形ABCD内，SO的长为3，O到AB，AD的距离分别为2和1，P是SC的中点．
（2008•湖北模拟）如图，已知四棱锥S-ABCD中，△SAD是边长为a的正三角形，平面SAD⊥平面ABCD，四边形ABCD为菱形，∠DAB=60°，P为AD的中点，Q为SB的中点．
（2010•江西模拟）（如图）已知四棱锥S-ABCD的底面ABCD是菱形，将面SAB，SAD，ABCD 展开成平面后的图形恰好为一正三角形S'SC．