题目内容
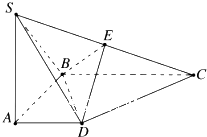
已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,点E是SC上任意一点.(Ⅰ)求证:平面EBD⊥平面SAC;
(Ⅱ)设SA=4,AB=2,求点A到平面SBD的距离;
(Ⅲ)当
| SA | AB |
分析:(1)欲证平面EBD⊥平面SAC,只需证BD⊥面SAC,利用线面垂直的判定定理可证得;
(2)过A作AF⊥SO交SO于点F,则AF⊥面SBD,所以线段AF的长就是点A到平面SBD的距离,利用等面积法求出线段AF的长即可;
(3)作BM⊥SC于M,连接DM,可证得∠BMD是二面角B-SC-D的平面角,利用余弦定理建立等量关系求解即可.
(2)过A作AF⊥SO交SO于点F,则AF⊥面SBD,所以线段AF的长就是点A到平面SBD的距离,利用等面积法求出线段AF的长即可;
(3)作BM⊥SC于M,连接DM,可证得∠BMD是二面角B-SC-D的平面角,利用余弦定理建立等量关系求解即可.
解答: 解:证明(Ⅰ)∵ABCD是正方形,∴BD⊥AC,
解:证明(Ⅰ)∵ABCD是正方形,∴BD⊥AC,
∵SA⊥底面ABCD,BD?面ABCD,∴SA⊥BD,
∵SA∩AC=A,∴BD⊥面SAC,
又∵BD?面EBD,∴平面EBD⊥平面SAC;(4分)
解:(Ⅱ)由(Ⅰ)知,BD⊥面SAC,又∵BD?面SBD,
∴平面SBD⊥平面SAC,设AC∩BD=O,
则平面SBD∩平面SAC=SO,过A作AF⊥SO交SO于点F,
则AF⊥面SBD,所以线段AF的长就是点A到平面SBD的距离.
∵ABCD是正方形,AB=2,∴AO=
,
又∵SA=4,△SAO是Rt△,∴SO=3
,
∵SO×AF=SA×AO,∴AF=
,∴点A到平面SBD的距离为
;(9分)
解:(Ⅲ)作BM⊥SC于M,连接DM,
∵SA⊥底面ABCD,AB=AD,∴SB=SD,
又∵CB⊥AB,CD⊥AD,∴CB⊥SB,CD⊥SD,
∴△SBC≌△SDC,∴DM⊥SC,
∴∠BMD是二面角B-SC-D的平面角,BM=DM.(11分)
要使∠BMD=120°,只须
=cos120°,
即BM2=
BD2,而BD2=2AB2,∴BM2=
AB2,
∵BM×SC=SB×BC,SC2=SB2+BC2,∴BM2×SC2=SB2×BC2,
∴
AB2(SB2+BC2)=SB2×BC2,
∵AB=BC,∴2SB2+2AB2=3SB2,∴SB2=2AB2,
又∵AB2=SB2-SA2,∴AB2=SA2,∴
=1,
故当
=1时,二面角B-SC-D的大小为120°.(14分)
 解:证明(Ⅰ)∵ABCD是正方形,∴BD⊥AC,
解:证明(Ⅰ)∵ABCD是正方形,∴BD⊥AC,∵SA⊥底面ABCD,BD?面ABCD,∴SA⊥BD,
∵SA∩AC=A,∴BD⊥面SAC,
又∵BD?面EBD,∴平面EBD⊥平面SAC;(4分)
解:(Ⅱ)由(Ⅰ)知,BD⊥面SAC,又∵BD?面SBD,
∴平面SBD⊥平面SAC,设AC∩BD=O,
则平面SBD∩平面SAC=SO,过A作AF⊥SO交SO于点F,
则AF⊥面SBD,所以线段AF的长就是点A到平面SBD的距离.
∵ABCD是正方形,AB=2,∴AO=
| 2 |
又∵SA=4,△SAO是Rt△,∴SO=3
| 2 |
∵SO×AF=SA×AO,∴AF=
| 4 |
| 3 |
| 4 |
| 3 |

解:(Ⅲ)作BM⊥SC于M,连接DM,
∵SA⊥底面ABCD,AB=AD,∴SB=SD,
又∵CB⊥AB,CD⊥AD,∴CB⊥SB,CD⊥SD,
∴△SBC≌△SDC,∴DM⊥SC,
∴∠BMD是二面角B-SC-D的平面角,BM=DM.(11分)
要使∠BMD=120°,只须
| BM2+DM2-BD2 |
| 2BM•DM |
即BM2=
| 1 |
| 3 |
| 2 |
| 3 |
∵BM×SC=SB×BC,SC2=SB2+BC2,∴BM2×SC2=SB2×BC2,
∴
| 2 |
| 3 |
∵AB=BC,∴2SB2+2AB2=3SB2,∴SB2=2AB2,
又∵AB2=SB2-SA2,∴AB2=SA2,∴
| SA |
| AB |
故当
| SA |
| AB |
点评:本题主要考查了平面与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=