题目内容
(普通文科做)已知f(x)=x3+bx2+9x+a有两个极值点,求:
(1)b的取值范围;
(2)当x=1时,切线的斜率为0.求f(x)的单调增区间.
(1)b的取值范围;
(2)当x=1时,切线的斜率为0.求f(x)的单调增区间.
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:计算题,导数的综合应用
分析:(1)由题意求导f′(x)=3x2+2bx+9,从而可得△=4b2-4×3×9>0,从而求得;
(2)令f′(1)=3+2b+9=0解得b=-6;从而求得f′(x)=3x2-12x+9=3(x-1)(x-3);根据导数的正负确定函数的单调性.
(2)令f′(1)=3+2b+9=0解得b=-6;从而求得f′(x)=3x2-12x+9=3(x-1)(x-3);根据导数的正负确定函数的单调性.
解答:
解:(1)∵f(x)=x3+bx2+9x+a,
∴f′(x)=3x2+2bx+9,
又∵f(x)=x3+bx2+9x+a有两个极值点,
∴△=4b2-4×3×9>0,
解得,b>3
或b<-3
;
(2)由题意,f′(1)=3+2b+9=0,
解得b=-6;
故f′(x)=3x2-12x+9=3(x-1)(x-3);
故当x>3或x<1时,f′(x)>0;
当1<x<3时,f′(x)<0;
故f(x)的单调增区间为(-∞,1),(3,+∞).
∴f′(x)=3x2+2bx+9,
又∵f(x)=x3+bx2+9x+a有两个极值点,
∴△=4b2-4×3×9>0,
解得,b>3
| 3 |
| 3 |
(2)由题意,f′(1)=3+2b+9=0,
解得b=-6;
故f′(x)=3x2-12x+9=3(x-1)(x-3);
故当x>3或x<1时,f′(x)>0;
当1<x<3时,f′(x)<0;
故f(x)的单调增区间为(-∞,1),(3,+∞).
点评:本题考查了导数的综合应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
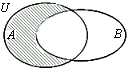 已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )
已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合为( )| A、{x|1≤x<3} |
| B、{x|x<3} |
| C、{x|x≤-1} |
| D、{x|-1<x<1} |
已知直线l1:3x-(k+2)y+6=0与直线l2:kx+(2k-3)y+2=0,记
.D=0是两条直线l1与直线l2平行的( )
|
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
某班有50名学生,某次数学考试成绩平均分为70分,标准差为s;后来发现记录有误,甲同学得70分误记为40分,乙同学得50分误记为80分,更正后重新计算的标准差为S1,则S与S1的大小关系为( )
| A、S>S1 |
| B、S<S1 |
| C、S=S1 |
| D、不能确定 |