题目内容
已知函数f(x)=x2-
ax3(a>0),x∈R.
(Ⅰ)求f(x)的单调区间和极值;
(Ⅱ)若对于任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)•f(x2)=1,求a的取值范围.
| 2 |
| 3 |
(Ⅰ)求f(x)的单调区间和极值;
(Ⅱ)若对于任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)•f(x2)=1,求a的取值范围.
考点:导数在最大值、最小值问题中的应用,函数在某点取得极值的条件,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)求导数,利用导数的正负,可得f(x)的单调区间,从而求出函数的极值;
(Ⅱ)由f(0)=f(
)=0及(Ⅰ)知,当x∈(0,
)时,f(x)>0;当x∈(
,+∞)时,f(x)<0.设集合A={f(x)|x∈(2,+∞)},集合B={
|x∈(1,+∞),f(x)≠0},则对于任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)•f(x2)=1,等价于A⊆B,分类讨论,即可求a的取值范围.
(Ⅱ)由f(0)=f(
| 3 |
| 2a |
| 3 |
| 2a |
| 3 |
| 2a |
| 1 |
| f(x) |
解答:
解:(Ⅰ)f′(x)=2x-2ax2=2x(1-ax),令f(x)=0,解得x=0或x=
.
当x变化时,f′(x),f(x)的变化情况如下表:
所以,f(x)的单调递减区间为:(-∞,0)和(
,+∞),单调递增区间为(0,
),
当x=0时,有极小值f(0)=0,当x=
时,有极大值f(
)=
;
(Ⅱ)由f(0)=f(
)=0及(Ⅰ)知,当x∈(0,
)时,f(x)>0;当x∈(
,+∞)时,f(x)<0.
设集合A={f(x)|x∈(2,+∞)},集合B={
|x∈(1,+∞),f(x)≠0},则对于任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)•f(x2)=1,等价于A⊆B,显然A≠∅
下面分三种情况讨论:
①当
>2,即0<a<
时,由f(
)=0可知,0∈A,而0∉B,∴A不是B的子集;
②当1≤
≤2,即
≤a≤
时,f(2)≤0,且f(x)在(2,+∞)上单调递减,故A=(-∞,f(2)),∴A⊆(-∞,0);由f(1)≥0,有f(x)在(1,+∞)上的取值范围包含(-∞,0),即(-∞,0)⊆B,∴A⊆B;
③当
<1,即a>
时,有f(1)<0,且f(x)在(1,+∞)上单调递减,故B=(
,0),A=(-∞,f(2)),∴A不是B的子集.
综上,a的取值范围是[
,
].
| 1 |
| a |
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (-∞,0) | 0 | (0,
|
| (
| ||||||
| f′(x) | - | 0 | + | 0 | - | ||||||
| f(x) | 递减 | 0 | 递增 |
| 递减 |
| 1 |
| a |
| 1 |
| a |
当x=0时,有极小值f(0)=0,当x=
| 1 |
| a |
| 1 |
| a |
| 1 |
| 3a2 |
(Ⅱ)由f(0)=f(
| 3 |
| 2a |
| 3 |
| 2a |
| 3 |
| 2a |
设集合A={f(x)|x∈(2,+∞)},集合B={
| 1 |
| f(x) |
下面分三种情况讨论:
①当
| 3 |
| 2a |
| 3 |
| 4 |
| 3 |
| 2a |
②当1≤
| 3 |
| 2a |
| 3 |
| 4 |
| 3 |
| 2 |
③当
| 3 |
| 2a |
| 3 |
| 2 |
| 1 |
| f(1) |
综上,a的取值范围是[
| 3 |
| 4 |
| 3 |
| 2 |
点评:利用导数可以求出函数的单调区间和极值;解决取值范围问题,很多时候要进行等价转化,分类讨论.

练习册系列答案
相关题目
已知集合A={1,zi},B={2},i为虚数单位,若A∩B=B,则纯虚数z为( )
| A、-i | B、-2i | C、i | D、2i |
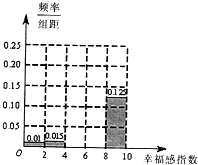 “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示:
“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示: