题目内容
已知抛物线 :
: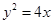 和
和 :
:
 的焦点分别为
的焦点分别为 ,
, 交于
交于 两点(
两点( 为坐标原点),且
为坐标原点),且
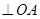 .
.
(1)求抛物线 的方程;
的方程;
(2)过点 的直线交
的直线交 的下半部分于点
的下半部分于点 ,交
,交 的左半部分于点
的左半部分于点 ,点
,点 坐标为
坐标为 ,求△
,求△ 面积的最小值.
面积的最小值.
(1)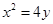 ;(2)8.
;(2)8.
解析试题分析:本题主要考查抛物线的标准方程及其几何性质、向量垂直的充要条件、两点间距离公式、三角形面积公式等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用抛物线的标准方程得到焦点 的坐标,从而得到向量
的坐标,从而得到向量 坐标,联立2个抛物线方程,解方程组,可求出A点坐标,从而得到向量
坐标,联立2个抛物线方程,解方程组,可求出A点坐标,从而得到向量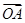 的坐标,由于
的坐标,由于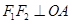 ,所以
,所以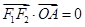 ,利用这个方程解出P的值,从而得到抛物线
,利用这个方程解出P的值,从而得到抛物线 的方程;第二问,先设出过点O的直线方程,直线和抛物线
的方程;第二问,先设出过点O的直线方程,直线和抛物线 联立,得到M点坐标,直线和抛物线
联立,得到M点坐标,直线和抛物线 联立得到N点坐标,由于
联立得到N点坐标,由于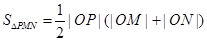 ,利用两点间距离公式得到3个边长,再利用基本不等式求面积的最小值.
,利用两点间距离公式得到3个边长,再利用基本不等式求面积的最小值.
试题解析:(1)由已知得: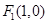 ,
,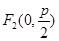 ,∴
,∴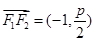 1分
1分
联立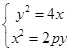 解得
解得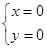 或
或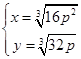 ,即
,即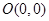 ,
,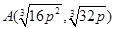 ,
,
∴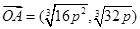 3分
3分
∵
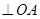 ,∴
,∴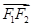
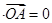 ,即
,即 ,解得
,解得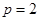 ,∴
,∴ 的方程为
的方程为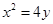 . 5分
. 5分
『法二』设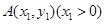 ,有
,有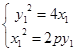 ①,由题意知,
①,由题意知,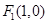 ,
,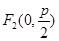 ,∴
,∴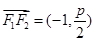 1分
1分
∵
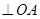 ,∴
,∴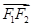
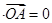 ,有
,有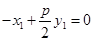 ,
,
解得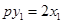 , 3分
, 3分
将其代入①式解得 ,从而求得
,从而求得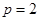 ,
,
所以 的方程为
的方程为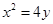 . 5分
. 5分
(2)设过 的直线方程为
的直线方程为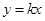
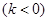
联立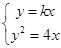 得
得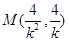 ,联立
,联立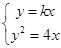 得
得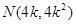 7分
7分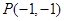 在直线
在直线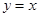 上,设点
上,设点 到直线
到直线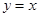 的距离为
的距离为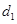 ,点
,点
练习册系列答案
相关题目
 )上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
)上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.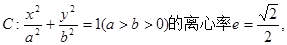 左、右焦点分别为F1、F2,点P(2,
左、右焦点分别为F1、F2,点P(2,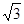 ),点F2在线段PF1的中垂线上.
),点F2在线段PF1的中垂线上. 与椭圆C交于M、N两点,直线F2M与F2N的斜率互为相反数,求证:直线l过定点,并求该定点的坐标.
与椭圆C交于M、N两点,直线F2M与F2N的斜率互为相反数,求证:直线l过定点,并求该定点的坐标.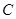 :
: 的一个焦点为
的一个焦点为 ,离心率为
,离心率为 .设
.设 是椭圆
是椭圆 的直线
的直线 交椭圆于
交椭圆于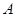 ,
, 两点.
两点. 的最大值.
的最大值. 的方程为
的方程为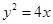 ,过原点作斜率为
,过原点作斜率为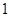 的直线和曲线
的直线和曲线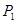 ,过
,过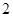 的直线与曲线
的直线与曲线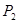 ,过
,过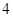 的直线与曲线
的直线与曲线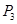 ,如此下去,一般地,过点
,如此下去,一般地,过点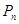 作斜率为
作斜率为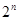 的直线与曲线
的直线与曲线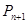 ,设点
,设点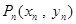 (
(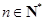 ).
).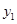 ,并求
,并求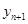 与
与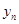 的关系式(
的关系式(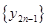 (
(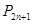 , 向哪一点无限接近?说明理由;
, 向哪一点无限接近?说明理由;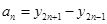 ,数列
,数列 的前
的前 项和为
项和为 ,设
,设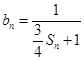 ,求所有可能的乘积
,求所有可能的乘积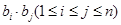 的和.
的和.
 的离心率为
的离心率为 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线 相切.
相切. 的方程;
的方程; ,过点
,过点 作与
作与 轴不重合的直线
轴不重合的直线 交椭圆于
交椭圆于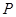 、
、 两点,连结
两点,连结 、
、 分别交直线
分别交直线 于
于 、
、 两点.试问直线
两点.试问直线 、
、 的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由.
的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由. 的左右顶点分别为
的左右顶点分别为 ,离心率
,离心率 .
. 为曲线
为曲线 :
: 上任一点(
上任一点( ),直线
),直线 与直线
与直线 交于点
交于点 ,
, 为线段
为线段 的中点,试判断直线
的中点,试判断直线 与曲线
与曲线 的右焦点为F,A为短轴的一个端点,且
的右焦点为F,A为短轴的一个端点,且 ,
, 的面积为1(其中
的面积为1(其中 为坐标原点).
为坐标原点). ,连结CM,交椭圆于点
,连结CM,交椭圆于点 ,证明:
,证明: 为定值;
为定值; 轴上是否存在异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,说明理由.
轴上是否存在异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,说明理由.