题目内容
13.球面上有不同的三点A、B、C,且AB=BC=AC=3,球心到A,B,C所在截面的距离为球半径的一半,则球的表面积为16π.分析 先确定ABC外接圆的半径,再求出球的半径,即可求得球的表面积.
解答  解:设球心为O,△ABC外接圆的圆心为O′,设球的半径为2r,则OO′=r,∴O′A=$\sqrt{3}$r
解:设球心为O,△ABC外接圆的圆心为O′,设球的半径为2r,则OO′=r,∴O′A=$\sqrt{3}$r
∵AB=BC=CA=3,∴O′A=$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$×3=$\sqrt{3}$,
∴$\sqrt{3}$r=$\sqrt{3}$
∴r=1
∴球的表面积4π•22=16π.
故答案为:16π.
点评 本题主要考查球的表面积,涉及到截面圆圆心与球心的连线垂直于截面,这是解题的关键.

练习册系列答案
相关题目
1.已知棱长为2,各面均为等边三角形的四面体S-ABC的各顶点都在球O的球面上,则球O的表面积为( )
| A. | π | B. | 2π | C. | 4π | D. | 6π |
 如图,已知点D为三角形ABC边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N*)为AC边上的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中,an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为三角形ABC边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N*)为AC边上的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中,an>0,a1=1,则{an}的通项公式为( )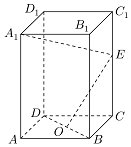 如图,正四棱柱ABCD-A1B1C1D1中,O是BD的中点,E是棱CC1上任意一点.
如图,正四棱柱ABCD-A1B1C1D1中,O是BD的中点,E是棱CC1上任意一点.