题目内容
2.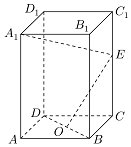 如图,正四棱柱ABCD-A1B1C1D1中,O是BD的中点,E是棱CC1上任意一点.
如图,正四棱柱ABCD-A1B1C1D1中,O是BD的中点,E是棱CC1上任意一点.(1)证明:BD⊥A1E;
(2)如果AB=2,$CE=\sqrt{2}$,OE⊥A1E,求AA1的长.
分析 (1)连结AC,A1C1,证明BD⊥平面ACC1A1得出BD⊥A1E;
(2)设AA1=a,求出△A1OE的边长,利用勾股定理列方程解出a.
解答 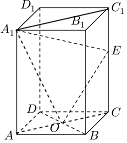 解:(1)证明:连结AC,A1C1,
解:(1)证明:连结AC,A1C1,
∵AA1⊥平面ABCD,BD?平面ABCD,
∴AA1⊥BD,
∵四边形ABCD是正方形,∴AC⊥BD,
又AC∩AA1=A,AC?平面ACC1A1,AA1?平面ACC1A1,
∴BD⊥平面ACC1A1,又A1E?平面ACC1A1,
∴BD⊥A1E.
(2)∵AB=2,∴AO=CO=$\sqrt{2}$,A1C1=2$\sqrt{2}$,
设AA1=a,则C1E=a-$\sqrt{2}$,
∴OE2=2+2=4,A1O2=a2+2,A1E2=(a-$\sqrt{2}$)2+8=a2-2$\sqrt{2}$a+10,
∵OE⊥A1E,
∴A1O2=OE2+A1E2,即a2+2=4+a2-2$\sqrt{2}$a+10,
解得a=3$\sqrt{2}$.∴AA1=3$\sqrt{2}$.
点评 本题考查了线面垂直的判定,棱柱的结构特征,属于中档题.

练习册系列答案
相关题目
17.某单位招聘员工,有200名应聘者参加笔试,随机抽查了其中20名应聘者笔试试卷,统计他们的成绩如下表:
若按笔试成绩择优录取40名参加面试,由此可预测参加面试的分数线为( )
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) | [90,95) |
| 人数 | 1 | 3 | 6 | 6 | 2 | 1 | 1 |
| A. | 70分 | B. | 75分 | C. | 80分 | D. | 85分 |
7.已知α是锐角,若cos(α+$\frac{π}{6}$)=$\frac{5}{13}$,则sin(α-$\frac{π}{12}$)=( )
| A. | -$\frac{17\sqrt{2}}{26}$ | B. | -$\frac{7\sqrt{2}}{26}$ | C. | $\frac{7\sqrt{2}}{26}$ | D. | $\frac{17\sqrt{2}}{26}$ |
17.某程序框图如图所示,对应的程序运行后输出的S的值是( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18.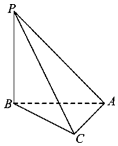 如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥P-ABC的外接球表面积为( )
如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥P-ABC的外接球表面积为( )
 如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥P-ABC的外接球表面积为( )
如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥P-ABC的外接球表面积为( )| A. | 3π | B. | 5π | C. | 12π | D. | 20π |