Question

14．在平行四平行边形OABC中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，点M在OA上，且$\overrightarrow{OM}$=2$\overrightarrow{MA}$，N为BC的中点，则$\overrightarrow{MN}$=（　　）

• A． $\frac{1}{2}$$\overrightarrow{c}$-$\frac{1}{6}$$\overrightarrow{a}$
• B． $\overrightarrow{c}$-$\frac{1}{6}$$\overrightarrow{a}$
• C． $\frac{3}{2}$$\overrightarrow{a}$-$\overrightarrow{c}$
• D． $\overrightarrow{a}$+$\frac{1}{2}$$\stackrel{c}{→}$

Answer 1

分析 画出图形，利用向量关系求解即可．

解答 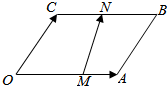解：在平行四边形OABC中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，点M在OA上，且$\overrightarrow{OM}$=2$\overrightarrow{MA}$，可得M是OA的三等分点，N为BC的中点，
可得$\overrightarrow{MN}$=$\overrightarrow{MO}$+$\overrightarrow{OC}$+$\frac{1}{2}\overrightarrow{CB}$=$-\frac{2}{3}\overrightarrow{a}$+$\overrightarrow{c}$$+\frac{1}{2}$$\overrightarrow{a}$=$\overrightarrow{c}-\frac{1}{6}\overrightarrow{a}$．
故选：B．

点评 本题考查四边形向量的加减法的应用，考查计算能力．