题目内容
已知数列{an}是等比数列,首项a1=2,a4=16.
(l)求数列{an}的通项公式;
(2)设数列bn=lgan,证明数列{bn}是等差数列并求前n项和Tn.
(l)求数列{an}的通项公式;
(2)设数列bn=lgan,证明数列{bn}是等差数列并求前n项和Tn.
考点:数列的求和,对数的运算性质,等差数列的前n项和,等比数列的通项公式
专题:计算题,等差数列与等比数列
分析:(l)等比数列{an}中,由a1=2,a4=16可求得公比q,从而可得数列{an}的通项公式;
(2)由(1)知bn=nlg2,易求bn-bn-1=lg2(n≥2),从而可证数列{bn}是等差数列并求前n项和Tn.
(2)由(1)知bn=nlg2,易求bn-bn-1=lg2(n≥2),从而可证数列{bn}是等差数列并求前n项和Tn.
解答:
解:(1)∵{an}是等比数列,a1=2,a4=16,
∴a1q3=16,q=2,
∴an=a1qn-1=2n.
(2)∵bn=lgan=lg2n=nlg2,
∴bn-bn-1=nlg2-(n-1)lg2=lg2(n≥2),
∴{bn}是以lg2为首项,以lg2为公差的等差数列.
∴Tn=
.
∴a1q3=16,q=2,
∴an=a1qn-1=2n.
(2)∵bn=lgan=lg2n=nlg2,
∴bn-bn-1=nlg2-(n-1)lg2=lg2(n≥2),
∴{bn}是以lg2为首项,以lg2为公差的等差数列.
∴Tn=
| (lg2)n(n+1) |
| 2 |
点评:本题考查数列的求和,着重考查等比数列的通项公式,考查等差关系的确定,属于中档题.

练习册系列答案
相关题目
已知条件p:x2-3x-4≤0,条件q:x2-6x+9-m2≤0(m>0).若p是q的充分不必要条件,则正数m的取值范围为( )
| A、(0,1] |
| B、(0,4] |
| C、[1,+∞) |
| D、[4,+∞) |
巳知等差数列{an}的公差d=1,若l,a1,a3成等比数列,则首项a1=( )
| A、-1 | B、-1或2 |
| C、2 | D、-2或1 |
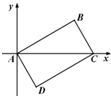 如图,在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标:A(0,0),B(3,
如图,在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标:A(0,0),B(3,