题目内容

1．已知p：函数y=lg（x2+mx+1）的值域为R．q：函数y=lg[4x2+4（m-2）x+1]的定义域为R．若p∨q为真，p∧q为假，求实数m的取值范围．

分析 若命题p是真命题，则△≥0，解得m范围．若命题q是真命题，则△＜0，解得m范围．若p∨q为真，p∧q为假，则p与q必然一真一假．即可得出．

解答 解：命题p：函数y=lg（x2+mx+1）的值域为R，∴△=m2-4≥0，解得m≥2或m≤-2．
命题q：函数y=lg[4x2+4（m-2）x+1]的定义域为R，∴△=16（m-2）2-16＜0，解得1＜m＜3．
若p∨q为真，p∧q为假，
则p与q必然一真一假．
∴$\left\{\begin{array}{l}{m≥2或m≤-2}\\{m≤1或m≥3}\end{array}\right.$，或$\left\{\begin{array}{l}{-2＜m＜2}\\{1＜m＜3}\end{array}\right.$，
解得m≤-2或m≥3，或1＜m＜2．
∴实数m的取值范围是m≤-2或m≥3，或1＜m＜2．

点评 本题考查了对数化为的单调性、二次函数的取值与判别式的关系、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
11．已知函数f（x）=2$\sqrt{3}$sinxcosx+1-2sin2x，x∈R，将函数y=f（x）的图象上各点的纵坐标缩短到原来的$\frac{1}{2}$，把所得到的图象再向左平移$\frac{π}{6}$个单位长度，得到函数y=g（x）的图象，求：
（I）函数g（x）的解析式和单调递增区间；
（Ⅱ）函数g（x）在区间[-$\frac{π}{6}$，-$\frac{π}{24}$]上的最值．
12．已知等比数列{an}中，a1-a3+a5=2，a3-a5+a7=5，那么a5-a7+a9=（　　）
A．8B．15C．25D．$\frac{25}{2}$
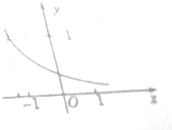9．已知AB是抛物线y2=4x的焦点弦，其端点A，B坐标分别为（x1，y1），（x2，y2）且满足x1+x2=6，则直线AB的斜率是±1．
16．函数f（x）=ax-b的函数图象如图所示，其中a和b的取值范围是0＜a＜1，b＜0．
6．已知函数f（x）=x2+6x+1，若关于x的不等式f（x）＜m在[-5，-2]上恒成立，则实数m的取值范围是（-4，+∞）．
13．对于数列{an}，a1=4，an+1=f（an），依照下表则a2015等于（　　）
X12345
F（x）54312
A．2B．3C．4D．5
10．已知f（x）为定义在（-1，1）上的奇函数，当x∈（0，1）时，f（x）=$\frac{{2}^{x}}{{4}^{x}+1}$．
（1）求f（x）在（-1，1）上的解析式；
（2）判断f（x）在（-1，1）上的单调性，并给予证明．
11．设曲线$\sqrt{\frac{{x}^{2}}{4{n}^{2}}}$+$\sqrt{{y}^{2}}$=1（n∈N*）所围成的平面区域Dn，记Dn内（含区域边界）的整点（整点即纵、横坐标均为整数的点）个数为an，数列{an}的前n项和为Sn．
（1）若a∈N*，且$\frac{{S}_{n}}{2n+5}$+$\frac{32}{{a}_{n}+1}$≥a恒成立，求a的最大值；
（2）在（1）a取最大值的条件下，当bn=$\frac{（a-2）^{n}•{S}_{n}}{（2n+5）}$时，求数列{bn}的前n项和Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网