Question

11．设曲线$\sqrt{\frac{{x}^{2}}{4{n}^{2}}}$+$\sqrt{{y}^{2}}$=1（n∈N^*）所围成的平面区域D_n，记D_n内（含区域边界）的整点（整点即纵、横坐标均为整数的点）个数为a_n，数列{aⁿ}的前n项和为S_n．
（1）若a∈N^*，且$\frac{{S}_{n}}{2n+5}$+$\frac{32}{{a}_{n}+1}$≥a恒成立，求a的最大值；
（2）在（1）a取最大值的条件下，当b_n=$\frac{（a-2）^{n}•{S}_{n}}{（2n+5）}$时，求数列{b_n}的前n项和T_n．

Answer 1

分析 （1）运用平面区域，求得数列的前几项，运用等差数列的求和公式，即可得到所求；
（2）由题意可得，a≤$\frac{n（2n+5）}{2n+5}$+$\frac{32}{4n+4}$=n+$\frac{8}{n+1}$，运用基本不等式，再由n=1，2，可得a的范围，进而得到a的最大值；
（3）化简数列{b_n}，再由错位相减法，计算即可得到所求．

解答 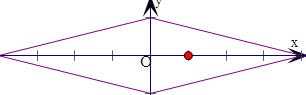解：（1）由平面区域D_n，可得，
当n=1时，a₁=7，当n=2时，a₂=11，
…，a_n=4n+3，
S_n=$\frac{1}{2}$n（4n+10）=n（2n+5），
$\frac{{S}_{n}}{2n+5}$+$\frac{32}{{a}_{n}+1}$≥a恒成立，
即为a≤$\frac{n（2n+5）}{2n+5}$+$\frac{32}{4n+4}$=n+$\frac{8}{n+1}$，
由n+$\frac{8}{n+1}$=n+1+$\frac{8}{n+1}$-1≥2$\sqrt{（n+1）•\frac{8}{n+1}}$-1
=4$\sqrt{2}$-1，
n+1=$\frac{8}{n+1}$，解得n=2$\sqrt{2}$-1∉N，
当n=1时，n+$\frac{8}{n+1}$=5；当n=2时，n+$\frac{8}{n+1}$=$\frac{14}{3}$，．
即有最小值为$\frac{14}{3}$，．
则a≤$\frac{14}{3}$，．即有a的最大值为4；
（2）b_n=$\frac{（a-2）^{n}•{S}_{n}}{（2n+5）}$=$\frac{{2}^{n}•n（2n+5）}{2n+5}$=n•2ⁿ，
前n项和T_n=1•2+2•4+…+n•2ⁿ，
2T_n=1•2²+2•8+…+n•2ⁿ⁺¹，
两式相减，可得-T_n=2+4+…+2ⁿ-n•2ⁿ⁺¹，
=$\frac{2（1-{2}^{n}）}{1-2}$-n•2ⁿ⁺¹，
化简可得，T_n=（n-1）•2ⁿ⁺¹+2．

点评 本题考查平面区域的画法及整点个数，考查等差数列和等比数列的求和公式的运用，考查数列的求和方法：错位相减法，考查不等式恒成立问题的解法，属于中档题．