题目内容


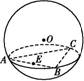
已知正三角形ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是(　　)

 (A)π (B)2π  (C)π  (D)3π


C:所作的截面与OE垂直时,截面圆的面积最小.设正三角形ABC的高为3a,

则4a2+1=4,

即a=,

此时OE2=12+=,截面圆半径r2=22-=,故截面面积为.故选C.


练习册系列答案
相关题目

设变量x,y满足约束条件,则目标函数z=3x-2y的最小值为（     ）（A）-5     （B）-4     （C）-2      （D）3

有一个面积为1 m2，形状为直角三角形的框架，有下列四种长度的钢管供应用，其中最合理(够用且最省)的是 (　　)

A．4.7 m        B．4.8 m      C．4.9 m          D．5 m

已知正三棱锥(底面是正三角形,各侧棱都相等的棱锥)VABC的正视图、侧视图和俯视图如图所示.

(1)画出该三棱锥的直观图;

(2)求出侧视图的面积.

某空间组合体的三视图如图所示,则该组合体的体积为(　)

(A)48   (B)56   (C)64   (D)72

如图所示,在边长为5+的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的表面积与体积.

下列说法正确的是(　 　)

(A)若a⊂α,b⊂β,则a与b是异面直线

(B)若a与b异面,b与c异面,则a与c异面

(C)若a,b不同在平面α内,则a与b异面

(D)若a,b不同在任何一个平面内,则a与b异面

设α,β是两个不同的平面,l,m为两条不同的直线,命题p:若α∥β,l⊂α,m⊂β,则l∥m;命题q:若l∥α,m⊥l,m⊂β,则α⊥β.下列命题为真命题的是(　　)

(A)p∨q      (B)p∧q  (C)(􀱑p)∨q   (D)p∧(􀱑q)

在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,).若S1,S2,S3分别为三棱锥DABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则(　)

(A)S1=S2=S3         (B)S2=S1且S2≠S3

(C)S3=S1且S3≠S2 (D)S3=S2且S3≠S1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网