题目内容
(本小题共13分)已知数列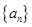 中,
中,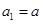 ,
, ,
,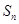 是数列
是数列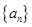 的前
的前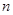 项和,且
项和,且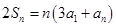 ,
,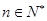 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求数列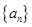 的通项公式;
的通项公式;
(Ⅲ)若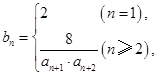
 是数列
是数列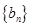 的前
的前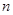 项和,求
项和,求 .
.
(Ⅰ)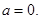 (Ⅱ)
(Ⅱ)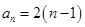 ,
,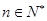 (Ⅲ)
(Ⅲ)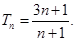
解析试题分析:(Ⅰ)因为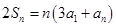 ,
,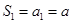 ,所以
,所以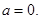 …2分
…2分
(Ⅱ)由(Ⅰ)可知 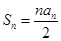 , 所以
, 所以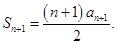
所以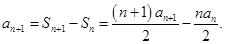 …3分
…3分
所以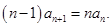 …5分
…5分
所以当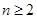 时,
时,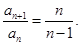
所以 ,
,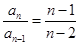 ,
, 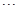 ,
,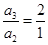 , … 6分
, … 6分
所以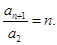 …7分
…7分
所以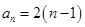 ,
,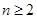 . …8分
. …8分
因为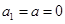 满足上式, …9分
满足上式, …9分
所以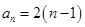 ,
,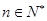 . …10分
. …10分
(Ⅲ)当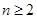 时,
时,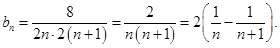 …11分
…11分
又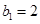 ,
,
所以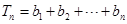
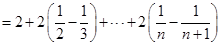 …12分
…12分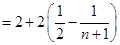
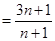
所以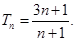 …13分
…13分
考点:本小题主要考查由数列的递推关系式求数列的通项公式和数列的前n项和公式的应用,考查学生分类讨论思想的应用.
点评:数列解答题是每年高考必考题型,以考查数列通项 、前n项和
、前n项和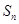 关系转化题型为主,考查通项公式、前n项和公式的应用能力及数列的性质掌握程度,解答此类题目,必须做到答题规范,尤其要注意n的取值范围.
关系转化题型为主,考查通项公式、前n项和公式的应用能力及数列的性质掌握程度,解答此类题目,必须做到答题规范,尤其要注意n的取值范围.

等比数列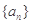 的前
的前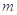 项和为4,前
项和为4,前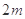 项和为12,则它的前
项和为12,则它的前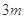 项和是
项和是
| A.28 | B.48 | C.36 | D.52 |
等差数列{an}中,若a1+a4+a7=39,a3+a6+a9=27,则前9项的和S9等于( ).
| A.66 | B.99 |
| C.144 | D.297 |
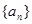 中,
中,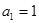 ,且
,且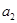 是
是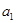 和
和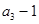 的等差中项.
的等差中项.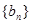 满足
满足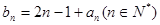 ,求
,求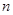 项和
项和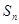 .
.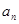 }的前n 项和为
}的前n 项和为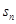 ,已知
,已知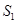 ,
,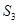 ,
,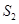 成等差数列
成等差数列 -
-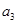 =3,求
=3,求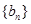 满足
满足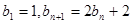 ,
,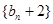 为等比数列 (2)求数列
为等比数列 (2)求数列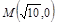 作直线
作直线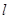 交曲线
交曲线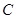 :
: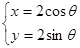 (
(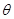 为参数)于
为参数)于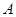 、
、 两点,若
两点,若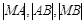 成等比数列,求直线
成等比数列,求直线 是公比大于1的等比数列,
是公比大于1的等比数列, 是函数
是函数 的两个零点。
的两个零点。 满足
满足 ,且
,且 ,求
,求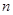 的最小值。
的最小值。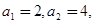 数列
数列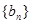 满足:
满足: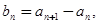
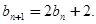
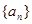 的通项公式.
的通项公式.