题目内容
9.设关于x的实系数不等式(ax+3)(x2-b)≤0对任意x∈[0,+∞)恒成立,则a2b=9.分析 利用换元法设f(x)=ax+3,g(x)=x2-b,根据一元一次函数和一元二次函数的图象和性质进行判断求解即可.
解答 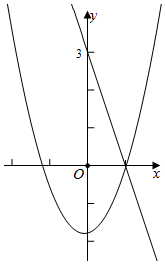 解:∵(ax+3)(x2-b)≤0对任意x∈[0,+∞)恒成立,
解:∵(ax+3)(x2-b)≤0对任意x∈[0,+∞)恒成立,
∴当x=0时,不等式等价为-3b≤0,即b≥0,
当x→+∞时,x2-b>0,此时ax+3<0,则a<0,
设f(x)=ax+3,g(x)=x2-b,
若b=0,则g(x)=x2>0,
函数f(x)=ax+3的零点为x=-$\frac{3}{a}$,则函数f(x)在(0,-$\frac{3}{a}$)上f(x)>0,此时不满足条件;
若a=0,则f(x)=3>0,而此时x→+∞时,g(x)>0不满足条件,故b>0;
∵函数f(x)在(0,-$\frac{3}{a}$)上f(x)>0,则(-$\frac{3}{a}$,+∞))上f(x)<0,
而g(x)在(0,+∞)上的零点为x=$\sqrt{b}$,且g(x)在(0,$\sqrt{b}$)上g(x)<0,
则($\sqrt{b}$,+∞)上g(x)>0,
∴要使(ax+3)(x2-b)≤0对任意x∈[0,+∞)恒成立,
则函数f(x)与g(x)的零点相同,即-$\frac{3}{a}$=$\sqrt{b}$,
∴a2b=9.
故答案为:9.
点评 本题考查了不等式恒成立以及分类讨论思想、转化与化归思想及运算求解能力,解题时应根据一元一次函数和一元二次函数的图象和性质,得到两个函数的零点相同,是较难的题目.

练习册系列答案
相关题目
19.已知定义域为R的奇函数y=f(x)的导函数为y=f′(x),当x≠0时,f′(x)+$\frac{f(x)}{x}$<0,若a=$\frac{1}{3}f(\frac{1}{3})$,b=-3f(-3),c=ln$\frac{1}{3}f(ln\frac{1}{3})$,则a,b,c的大小关系正确的是( )
| A. | a<b<c | B. | b<c<a | C. | a<c<b | D. | c<a<b |
17.已知集合A={x|x≤0,x∈R},B={a,1},若A∩B≠∅,则实数a的取值范围是( )
| A. | a<1 | B. | a≤1 | C. | a≥0 | D. | a≤0 |
19.复数z=$\frac{-i}{4+i}$(其中i为虚数单位)的虚部为( )
| A. | -$\frac{1}{17}$ | B. | $\frac{4}{17}$ | C. | -$\frac{4}{17}$i | D. | -$\frac{4}{17}$ |