题目内容
(本小题满分12分)
设函数f (x)=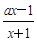 ,其中a∈R.
,其中a∈R.
(1)若a=1,f (x)的定义域为[0,3],求f (x)的最大值和最小值.
(2)若函数f (x)的定义域为区间(0,+∞),求a的取值范围使f (x)在定义域内是单调减函数.
设函数f (x)=
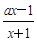 ,其中a∈R.
,其中a∈R.(1)若a=1,f (x)的定义域为[0,3],求f (x)的最大值和最小值.
(2)若函数f (x)的定义域为区间(0,+∞),求a的取值范围使f (x)在定义域内是单调减函数.
(1)f (x)max= ,f (x)min=-1;(2)a<-1。
,f (x)min=-1;(2)a<-1。
 ,f (x)min=-1;(2)a<-1。
,f (x)min=-1;(2)a<-1。试题分析:f (x)=
 =
= =a-
=a- ,
,设x1,x2∈R,则f (x1)-f (x2)=
 =
= . ……2分
. ……2分(1)当a=1时,设0≤x1<x2≤3,则f (x1)-f (x2)=
 .
.又x1-x2<0,x1+1>0,x2+1>0,所以f (x1)-f (x2)<0,
∴f (x1)<f (x2), ……4分
所以f (x)在[0,3]上是增函数,所以f (x)max=f (3)=1-
 =
= ;
;f (x)min=f (0)=1-
 =-1. ……7分
=-1. ……7分(2)设x1>x2>0,则x1-x2>0,x1+1>0,x2+1>0
要f (x)在(0,+∞)上是减函数,只要f (x1)-f (x2)<0
而f (x1)-f (x2)=
 ,所以当a+1<0即a<-1时,有f (x1)-f (x2)<0,所以f (x1)<f (x2),
,所以当a+1<0即a<-1时,有f (x1)-f (x2)<0,所以f (x1)<f (x2),所以当a<-1时,f (x)在定义域(0,+∞)上是单调减函数. ……12分
点评:对于形如
 的函数,我们常采取分离常数法化为
的函数,我们常采取分离常数法化为 的形式。而
的形式。而 的图像可以有反比例函数的图像经过平移伸缩变换得到。
的图像可以有反比例函数的图像经过平移伸缩变换得到。
练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
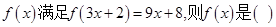


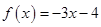
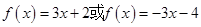
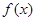 对于其定义域内的某一数
对于其定义域内的某一数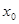 ,有
,有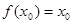 ,则称
,则称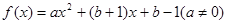 .
.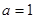 ,
, 时,求函数
时,求函数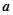 的取值范围;
的取值范围;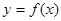 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数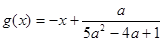 的图象上,求实数b的最小值.
的图象上,求实数b的最小值.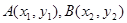 ,则线段AB的中点坐标为
,则线段AB的中点坐标为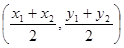 )
)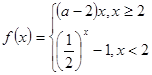 是R是的单调递减函数,则实数
是R是的单调递减函数,则实数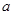 的取值范围是( )
的取值范围是( )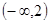
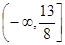
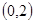
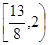
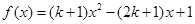 ,
, .
.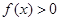 恒成立,求实数
恒成立,求实数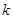 的取值范围;
的取值范围;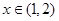 时,
时,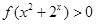 恒成立,求实数
恒成立,求实数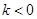 时,解不等式
时,解不等式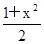 对一切实数x均成立?
对一切实数x均成立?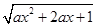 的定义域为R,解关于x的不等式
的定义域为R,解关于x的不等式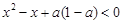
 的图象关于( )对称
的图象关于( )对称