题目内容
(本题满分16分)设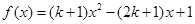 ,
, .
.
(1)若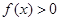 恒成立,求实数
恒成立,求实数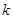 的取值范围;
的取值范围;
(2)若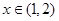 时,
时,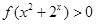 恒成立,求实数
恒成立,求实数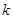 的取值范围;
的取值范围;
(3)当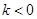 时,解不等式
时,解不等式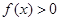 .
.
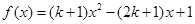 ,
, .
.(1)若
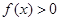 恒成立,求实数
恒成立,求实数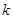 的取值范围;
的取值范围;(2)若
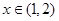 时,
时,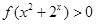 恒成立,求实数
恒成立,求实数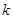 的取值范围;
的取值范围;(3)当
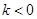 时,解不等式
时,解不等式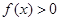 .
.(1)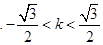 ;
;
(2)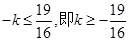 .
.
(3)1)当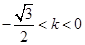 时,原不等式解为一切实数;
时,原不等式解为一切实数;
2)当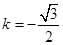 时,原不等式解为:
时,原不等式解为: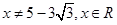 .
.
3)当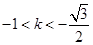 时,原不等式的解为:
时,原不等式的解为: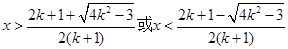 ;
;
4)当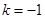 时,原不等式的解为:
时,原不等式的解为: ;
;
5)当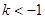 时,
时, 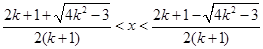 。
。
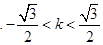 ;
;(2)
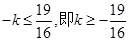 .
.(3)1)当
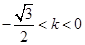 时,原不等式解为一切实数;
时,原不等式解为一切实数; 2)当
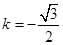 时,原不等式解为:
时,原不等式解为: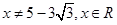 .
.3)当
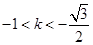 时,原不等式的解为:
时,原不等式的解为: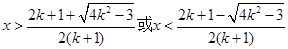 ;
; 4)当
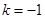 时,原不等式的解为:
时,原不等式的解为: ;
;5)当
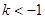 时,
时, 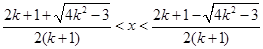 。
。试题分析:(1) 因为
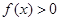 恒成立,所以k=-1时显然不成立;那么k应满足
恒成立,所以k=-1时显然不成立;那么k应满足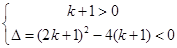 ,解之得即可求得k的取值范围.
,解之得即可求得k的取值范围.(2)当
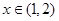 时,
时,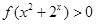 恒成立,设
恒成立,设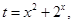 因为它在(1,2)上是增函数,故
因为它在(1,2)上是增函数,故 ,
,从而当
 时,
时,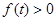 恒成立,因而转化为常规的一元二次不等式
恒成立,因而转化为常规的一元二次不等式 对于
对于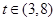 恒成立来解决即可.
恒成立来解决即可.(3)
 ,然后根据
,然后根据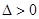 和
和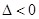 和
和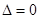 再结合k<0分三种情况讨论解不等式即可.
再结合k<0分三种情况讨论解不等式即可.(1)
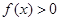 恒成立
恒成立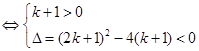 ……
……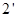
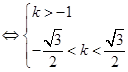 ,
,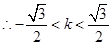 ……
……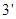
(2)令
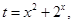 它在(1,2)上是增函数,故
它在(1,2)上是增函数,故 ,
,从而当
 时,
时,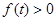 恒成立 ……
恒成立 ……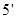
即
 对于
对于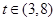 恒成立,
恒成立,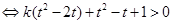 ;因为当
;因为当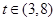 时,
时,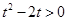 ,
,所以
 , ……
, ……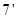
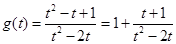 ,
,令
 ,则
,则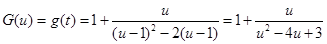
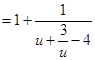 , ……
, ……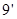
而
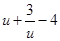 在
在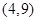 上是增函数,且
上是增函数,且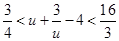 ,
,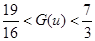 ,从而
,从而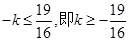 . ……
. ……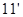
(3)
 ,
,1)当
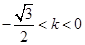 时,
时, ,原不等式解为一切实数;
,原不等式解为一切实数; 2)当
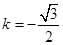 时,
时,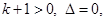 原不等式解为:
原不等式解为: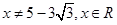 .
.3)当
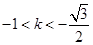 时,
时,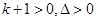 ,
,原不等式的解为:
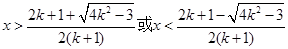 ;……
;……
4)当
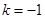 时,原不等式的解为:
时,原不等式的解为: ;
;5)当
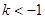 时,
时,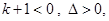
原不等式的解为:
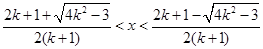 ……
……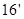 .
.点评:(1)对于一元二次不等式f(x)>0恒成立问题,要满足开口向上,并且与x轴无交点,所以
二次项系数大于零,并且
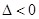 .
.(2)对于复杂类型的不等式问题可考虑采用换元法转化为常见不等式类型求解.
(3)对于含参的一元二次不等式要注意根据
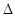 的符号分类讨论求解.
的符号分类讨论求解.
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
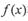 和,
和,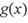 ,若对任意的
,若对任意的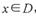 ,都有
,都有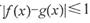 ,则称
,则称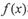 和
和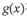 在D上是“密切函数”.给出定义域均为
在D上是“密切函数”.给出定义域均为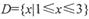 的四组函数:、
的四组函数:、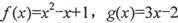
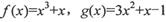
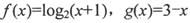
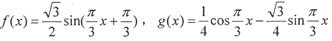
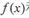 与
与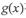 在D上为“密切函数”的是_______.
在D上为“密切函数”的是_______. ,
,
 是偶函数,求
是偶函数,求 的值。
的值。 ,
, ,求
,求 的最小值。
的最小值。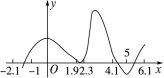
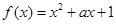 是偶函数,则函数
是偶函数,则函数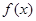 的最小值为 .
的最小值为 .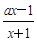 ,其中a∈R.
,其中a∈R.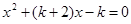 的两实根均在区间(
的两实根均在区间(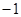 ,1)内,求
,1)内,求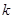 的取值范围 。
的取值范围 。
 的最小值;
的最小值;  的值域。
的值域。