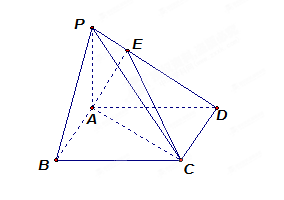
题目内容
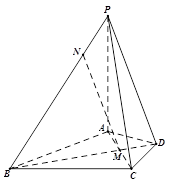
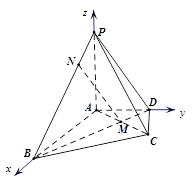
在四棱锥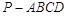 中,
中,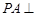 平面
平面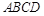 ,
,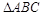 是正三角形,
是正三角形,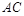 与
与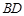 的交点
的交点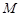 恰好是
恰好是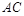 中点,又
中点,又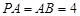 ,
,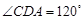 ,点
,点 在线段
在线段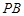 上,且
上,且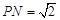 .
.
(1)求证: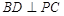 ;
;
(2)求证: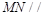 平面
平面 ;
;
(3)求二面角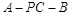 的余弦值.
的余弦值.
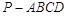 中,
中,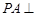 平面
平面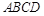 ,
,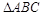 是正三角形,
是正三角形,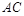 与
与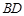 的交点
的交点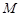 恰好是
恰好是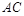 中点,又
中点,又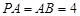 ,
,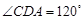 ,点
,点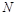 在线段
在线段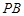 上,且
上,且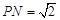 .
.
(1)求证:
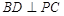 ;
;(2)求证:
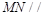 平面
平面 ;
;(3)求二面角
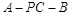 的余弦值.
的余弦值.(1)详见解析;(2)详见解析;(3)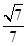
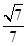
试题分析:(1)线线垂直是通过线面垂直证明,由已知
 ,
, ,从而
,从而 平面
平面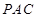 ,进而可证明
,进而可证明 ;(2)要证明直线和平面平行,只需在平面内找一条直线与之平行即可,该题中通过计算得
;(2)要证明直线和平面平行,只需在平面内找一条直线与之平行即可,该题中通过计算得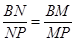 ,从而说明
,从而说明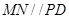 ,进而证明
,进而证明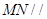 面
面 ;(3)二面角的求法:根据已知条件选三条两两垂直的直线,分别作为
;(3)二面角的求法:根据已知条件选三条两两垂直的直线,分别作为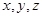 轴,建立空间直角坐标系,表示相关点的坐标,并求二面角两个半平面的法向量,再求法向量的夹角,通过观察二面角是锐二面角还是钝二面角,决定二面角余弦值的正负,该题中,可选
轴,建立空间直角坐标系,表示相关点的坐标,并求二面角两个半平面的法向量,再求法向量的夹角,通过观察二面角是锐二面角还是钝二面角,决定二面角余弦值的正负,该题中,可选 的方向为
的方向为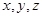 轴的正方向,而且面
轴的正方向,而且面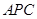 的法向量就是
的法向量就是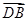 ,故只需求面
,故只需求面 的法向量即可.
的法向量即可.试题解析:(I) 因为
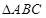 是正三角形,
是正三角形,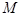 是
是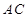 中点,所以
中点,所以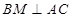 ,即
,即 ,又因为
,又因为 ,
, 平面
平面 ,
, ,又
,又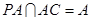 ,所以
,所以 平面
平面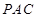 ,
,又
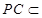 平面
平面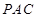 ,所以
,所以 .
.(Ⅱ)在正三角形
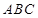 中,
中,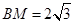 , 在
, 在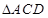 中,因为
中,因为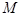 为
为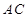 中点,
中点, ,所以
,所以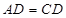
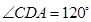 ,所以
,所以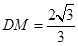 ,所以
,所以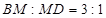 ,在等腰直角三角形
,在等腰直角三角形 中,
中,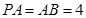 ,
,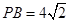 ,所以
,所以 ,
,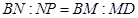 ,所以
,所以 ,又
,又 平面
平面 ,
,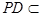 平面
平面 ,所以
,所以 平面
平面 .
.
(Ⅲ)因为
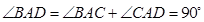 ,所以
,所以 ,分别以
,分别以 为
为 轴,
轴, 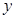 轴,
轴, 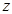 轴建立如图的空间直角坐标系,所以
轴建立如图的空间直角坐标系,所以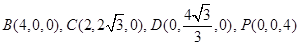
由(Ⅱ)可知,
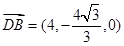 为平面
为平面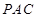 的法向量 ,
的法向量 ,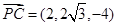 ,
,
设平面
 的一个法向量为
的一个法向量为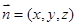 ,则
,则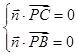 ,即
,即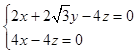 ,令
,令 则平面
则平面 的一个法向量为
的一个法向量为 , 设二面角
, 设二面角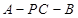 的大小为
的大小为 , 则
, 则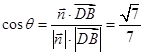
所以二面角
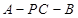 余弦值为
余弦值为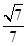 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 中,底面
中,底面 是边长为
是边长为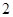 的正方形,
的正方形,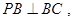
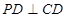 ,且
,且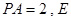 点满足
点满足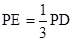 .
. 
 平面
平面 上是否存在点
上是否存在点 ,使得
,使得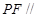 平面
平面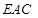 ?若存在,确定点
?若存在,确定点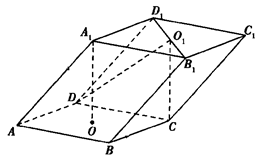
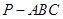 中,
中,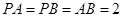 ,
,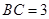 ,
,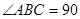 °,平面
°,平面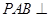 平面
平面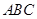 ,
,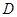 、
、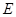 分别为
分别为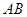 、
、 中点.
中点.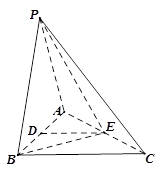
 ∥平面
∥平面 ;
;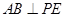 ;
; 的大小.
的大小.



 是两个不同的平面,
是两个不同的平面, 是一条直线,则下列命题正确的是( )
是一条直线,则下列命题正确的是( )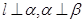 ,则
,则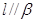
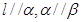 ,则
,则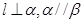 ,则
,则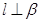
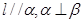 ,则
,则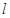 上有无数个点不在平面
上有无数个点不在平面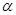 内,则
内,则