题目内容
设f(x)是定义在R上的偶函数，对任意x∈R，都有f(x－2)＝f(x＋2)，且当x∈[－2,0]时，f(x)＝(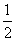
)x－1，若在区间(－2,6]内关于x的方程f(x)－loga(x＋2)＝0(a>1)恰有3个不同的实数根，则a的取值范围是________．
(
，2)
解析 由f(x－2)＝f(x＋2)，知f(x)是周期为4的周期函数，于是可得f(x)在(－2,6]上的草图如图中实线所示，
而函数g(x)＝loga(x＋2)(a>1)的图象如图中虚线所示，
结合图象可知，要使得方程f(x)－loga(x＋2)＝0(a>1)在区间(－2,6]内恰有3个不同的实数根，
必需且只需
解得<a<2.
练习册系列答案
相关题目
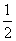<2x<8，x∈R}，B＝{x|－1<x<m＋1，x∈R}，若x∈B成立的一个充分不必要的条件是x∈A，则实数m的取值范围是________．
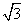cos ωx)，其中0<ω<2.函数f(x)＝a·b－
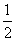，其图象的一条对称轴为x＝
.
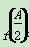＝1，b＝1，S△ABC＝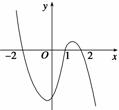
B．
C．
D．
，若
下列结论中正确的是（ ）
B．
D．
的定义域为
，则函数
的定义域为 ；
依次表示方程
，
，
的根，
B.
C.
D.