题目内容
已知三个元素3，x，x2-2x构成一个集合，则实数x应满足的条件为 ．
考点：集合的含义
专题：函数的性质及应用
分析：本题根据集合中元素的互异性，得到相应的不等式关系式，解不等式，可得到本题的结论．
解答：
解：∵根据集合中元素的互异性，
∴
，
∴x≠3且x≠0且x≠-1．
故答案：x≠3且x≠0且x≠-1．
∴
|
∴x≠3且x≠0且x≠-1．
故答案：x≠3且x≠0且x≠-1．
点评：本题考查了集合中元素的互异性，本题思维量小，属于基础题．
练习册系列答案
相关题目
已知点（1，-1）和（-2，1）在直线3x-2y-a=0的两侧，则a的取值范围是（ ）
| A、（-5，8） |
| B、（-8，5） |
| C、（-∞，-5）∪（8，+∞） |
| D、（-∞，-8）∪（5，+∞） |
已知集合A={x|x≥4}，g（x）=
的定义域为B，若A∩B=∅，则实数a的取值范围是（ ）
| 1 | ||
|
| A、（-2，4） |
| B、（3，+∞） |
| C、（-∞，3） |
| D、（-∞，3] |
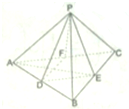如图，在所有棱长都相等的正三棱锥P-ABC中，D，E，F分别是AB，BC，CA的中点，下列四个结论不成立的是（ ）| A、BC∥平面PDF |
| B、平面PDF⊥平面ABC |
| C、平面PAE⊥平面ABC |
| D、平面PDF⊥平面PAE |