题目内容
已知3
-2
=(-2,0,4),
=(-2,1,2),|
|=4,θ为向量
与
的夹角.
(1)当
?
=2时,求θ的值;
(2)设
?
=m,m∈R,m为何值时,θ的值最大?此时
的坐标为多少?
| a |
| b |
| c |
| b |
| b |
| c |
(1)当
| a |
| c |
(2)设
| a |
| c |
| b |
考点:平面向量数量积的运算
专题:空间向量及应用
分析:(1)根据题意,求出
与
的夹角的余弦值cosθ的值,利用反三角函数求出θ的值;
(2)当
?
=m时,求出cosθ的表达式,根据cosθ的取值范围,求出m的值,再求对应的向量
即可.
| b |
| c |
(2)当
| a |
| c |
| b |
解答:
解:(1)∵3
-2
=(-2,0,4),
=(-2,1,2),|
|=4,
?
=2,θ为向量
与
的夹角,
∴(3
-2
)•
=3
•
-2
•
=3×2-2
•
=-2×(-2)+0×1+4×2=12,
∴
•
=-3,
∴4×
cosθ=-3,
解得cosθ=-
;
又∵θ∈[0,π],
∴θ=π-arccos
;
(2)当
?
=m时,由(1)知,
(3
-2
)•
=3
•
-2
•
=3m-2
•
=12,
∴
•
=
m-6,
∴4×3cosθ=
m-6,
∴cosθ=
m-
;
又∵θ∈[0,π],
令
m-
=-1,得:
当m=-4时,θ=π最大,
此时设
=(-2x,x,2x),
∴(-2x)2+x2+(2x)2=9x2=4,
∴x=±
;
∵θ=π,
∴
=(
,-
,-
).
| a |
| b |
| c |
| b |
| a |
| c |
| b |
| c |
∴(3
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| b |
| c |
∴
| b |
| c |
∴4×
| (-2)2+12+22 |
解得cosθ=-
| 1 |
| 4 |
又∵θ∈[0,π],
∴θ=π-arccos
| 1 |
| 4 |
(2)当
| a |
| c |
(3
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| b |
| c |
∴
| b |
| c |
| 3 |
| 2 |
∴4×3cosθ=
| 3 |
| 2 |
∴cosθ=
| 1 |
| 8 |
| 1 |
| 2 |
又∵θ∈[0,π],
令
| 1 |
| 8 |
| 1 |
| 2 |
当m=-4时,θ=π最大,
此时设
| b |
∴(-2x)2+x2+(2x)2=9x2=4,
∴x=±
| 2 |
| 3 |
∵θ=π,
∴
| b |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
点评:本题考查了空间向量的应用问题,也考查了利用向量的数量积求夹角的问题和计算能力,是中档题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、4 | ||
B、4+
| ||
| C、8+π | ||
D、2+
|
已知函数f(x)=sin(
x+
),则f(x)的最小正周期和初相φ分别为 ( )
| π |
| 3 |
| π |
| 6 |
A、T=6π,φ=
| ||
B、T=6π,φ=
| ||
C、T=6,φ=
| ||
D、T=6,φ=
|
下列结论成立的是( )
| A、若ac>bc,则a>b |
| B、若a>b,则a2>b2 |
| C、若a>b,c<d,则a+c>b+d |
| D、若a>b,c>d,则a-d>b-c |
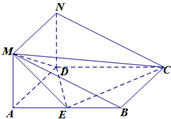 如图所示的几何体中,四边形ABCD为菱形,AMND是矩形,平面AMND⊥平面ABCD,∠DAB=60°,AD=2,AM=1.
如图所示的几何体中,四边形ABCD为菱形,AMND是矩形,平面AMND⊥平面ABCD,∠DAB=60°,AD=2,AM=1.