题目内容

12．二项式（x-$\frac{1}{2x}$）9展开式中，x3项的系数为（　　）
A．-$\frac{5}{2}$B．$\frac{5}{2}$C．-$\frac{21}{2}$D．$\frac{21}{2}$

分析 利用通项公式即可得出．

解答 解：二项式（x-$\frac{1}{2x}$）9展开式中，通项公式Tr+1=${∁}_{9}^{r}$${x}^{9-r}（-\frac{1}{2x}）^{r}$=$（-\frac{1}{2}）^{r}$${∁}_{9}^{r}$x9-2r，
令9-2r=3，解得r=3，
x3项的系数=$（-\frac{1}{2}）^{3}$${∁}_{9}^{3}$=-$\frac{21}{2}$．
故选：C．

点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
2．设集合M={x|x≥2}，N={x|x2-25＜0}，则M∩N=（　　）
A．（1，5）B．[2，5）C．（-5，2]D．[2，+∞）
3．已成椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右顶点分别为A1、A2，上下顶点分别为B2/B1，左右焦点分别为F1、F2，其中长轴长为4，且圆O：x2+y2=$\frac{12}{7}$为菱形A1B1A2B2的内切圆．
（1）求椭圆C的方程；
（2）点N（n，0）为x轴正半轴上一点，过点N作椭圆C的切线l，记右焦点F2在l上的射影为H，若△F1HN的面积不小于$\frac{3}{16}$n2，求n的取值范围．
20．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x，x＞0}\\{{3}^{x}，x≤0}\end{array}\right.$，则f（f（2））的值为（　　）
A．-$\frac{1}{3}$B．-3C．$\frac{1}{3}$D．3
7．两个单位向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$⊥$\overrightarrow{b}$，且$\overrightarrow{a}$⊥（x$\overrightarrow{a}$+$\overrightarrow{b}$），则|2$\overrightarrow{a}$-（x+1）$\overrightarrow{b}$|=$\sqrt{5}$．
17．设向量$\overrightarrow{OA}$=（1，-2），$\overrightarrow{OB}$=（a，-1），$\overrightarrow{OC}$=（-b，0），其中 O 为坐标原点，b＞0，若 A，B，C 三点共线，则$\frac{1}{a}$+$\frac{2}{b}$的最小值为（　　）
A．4B．6C．8D．9
4．设椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的一个顶点抛物线${x^2}=4\sqrt{3}y$的焦点重合，F1与F2分别是该椭圆的左右焦点，离心率$e=\frac{1}{2}$，且过椭圆右焦点F2的直线l与椭圆C交于M．N两点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若$\overrightarrow{OM}•\overrightarrow{ON}=-2$，其中O为坐标原点，求直线l的方程；
（Ⅲ）若AB椭圆C经过原点O的弦，且MN∥AB，判断$\frac{{{{|{AB}|}^2}}}{{|{MN}|}}$是否为定值？若是定值，请求出，若不是定值，说明理由．
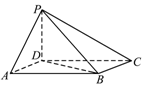1．如图，四棱锥P-ABCD中，底面ABCD为平行四边形，AB=2AD=2，$∠DAB=\frac{π}{3}$，PD⊥AD，PD⊥DC．
（Ⅰ）证明：平面PBC⊥平面PBD；
（Ⅱ）若二面角P-BC-D为$\frac{π}{6}$，求AP与平面PBC所成角的正弦值．
2．设函数f（x）=|2x+3|-|2x-a|，a∈R．
（1）若不等式f（x）≤-5的解集非空，求实数a的取值范围；
（2）若函数y=f（x）的图象关于点（-$\frac{1}{2}$，0）对称，求实数a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网