题目内容
2.在△ABC中,|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{AB}$-$\overrightarrow{AC}$|,AC=1,BC=$\sqrt{3}$,M是边BC上靠近C的一个四等分点,若N是BC边上的动点,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的取值范围是[$\frac{1}{2}$,$\frac{3}{4}$].分析 由|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{AB}$-$\overrightarrow{AC}$|得$\overrightarrow{AB}⊥\overrightarrow{AC}$,建立平面直角坐标系,设N坐标,求出$\overrightarrow{AN},\overrightarrow{AM}$的坐标,根据x的范围求出.
解答 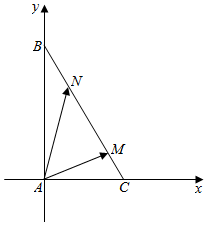 解:∵|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{AB}$-$\overrightarrow{AC}$|,∴$\overrightarrow{AB}⊥\overrightarrow{AC}$,∴AB=$\sqrt{2}$.
解:∵|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{AB}$-$\overrightarrow{AC}$|,∴$\overrightarrow{AB}⊥\overrightarrow{AC}$,∴AB=$\sqrt{2}$.
以AC,AB为坐标轴建立平面直角坐标系,
则A(0,0),C(1,0),B(0,$\sqrt{2}$),
∵M是边BC上靠近C的一个四等分点,∴M($\frac{3}{4}$,$\frac{\sqrt{2}}{4}$).
直线BC方程为x+$\frac{y}{\sqrt{2}}$=1,即$\sqrt{2}$x+y-$\sqrt{2}$=0.
设N(x,$\sqrt{2}-\sqrt{2}x$),则0≤x≤1,
则$\overrightarrow{AM}$=($\frac{3}{4}$,$\frac{\sqrt{2}}{4}$),$\overrightarrow{AN}$=(x,$\sqrt{2}-\sqrt{2}x$).
∴$\overrightarrow{AM}$•$\overrightarrow{AN}$=$\frac{3x}{4}$+$\frac{1}{2}$-$\frac{x}{2}$=$\frac{x}{4}$+$\frac{1}{2}$.
∵0≤x≤1,∴$\frac{1}{2}$≤$\overrightarrow{AM}$•$\overrightarrow{AN}$≤$\frac{3}{4}$.
故答案为[$\frac{1}{2}$,$\frac{3}{4}$].
点评 本题考查了平面向量的数量积运算,建立坐标系使用坐标计算是常用方法.

 (B类题)如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=$\sqrt{3}$AB,则下列结论正确的是( )
(B类题)如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=$\sqrt{3}$AB,则下列结论正确的是( )| A. | PB⊥AD | B. | 平面PAB⊥平面PBC | ||
| C. | 直线BC∥平面PAE | D. | △PFB为等边三角形 |
 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,已知椭圆C的焦距为2,且|AB|=$\frac{\sqrt{6}}{2}$|BF|.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,已知椭圆C的焦距为2,且|AB|=$\frac{\sqrt{6}}{2}$|BF|.