题目内容
10.设方程x2+px+q=0的两根是tanθ和tan($\frac{π}{4}$-θ).且方程的这两个根之比为3:2,求p和q的值.分析 由tanθ和tan($\frac{π}{4}$-θ)是方程x2+px+q=0的两个根,且这两个根之比为3:2列式求出tanθ,进一步求得tan($\frac{π}{4}$-θ),再由根与系数的关系求得p和q的值.
解答 解:∵tanθ和tan($\frac{π}{4}$-θ)是方程x2+px+q=0的两个根,且这两个根之比为3:2,
得$\frac{tanθ}{tan(\frac{π}{4}-θ)}=\frac{tanθ}{\frac{1-tanθ}{1+tanθ}}=\frac{3}{2}$,解得:tanθ=-3或tan$θ=\frac{1}{2}$,
则tan($\frac{π}{4}$-θ)=-2或tan($\frac{π}{4}$-θ)=$\frac{1}{3}$.
由根与系数的关系可得:p=5,q=6或p=-$\frac{5}{6},q=\frac{1}{6}$.
点评 本题考查学生运用两角和与差的正切函数的能力,以及利用一元二次方程的根的分布与系数关系的能力,是中档题.

练习册系列答案
相关题目
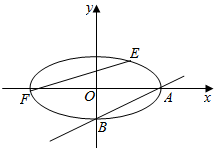 已知椭圆线$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,如图所示,A(a,0),B(0,-b)原点到直线AB的距离为$\frac{4}{\sqrt{5}}$.
已知椭圆线$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,如图所示,A(a,0),B(0,-b)原点到直线AB的距离为$\frac{4}{\sqrt{5}}$. 如图所示,AE,DF是圆柱的两条母线,过AD作圆柱的截面交下底面于BC,且AD=BC,圆柱的高为2,底面半径为$\sqrt{3}$
如图所示,AE,DF是圆柱的两条母线,过AD作圆柱的截面交下底面于BC,且AD=BC,圆柱的高为2,底面半径为$\sqrt{3}$