题目内容

19．（B类题）如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC，PA=$\sqrt{3}$AB，则下列结论正确的是（　　）
A．PB⊥ADB．平面PAB⊥平面PBC
C．直线BC∥平面PAED．△PFB为等边三角形

分析 利用题中条件，逐一分析答案，通过排除和筛选，得到正确答案．

解答 解：∵AD与PB在平面的射影AB不垂直，
∴A不成立，
又平面PAB⊥平面PAE，
∴平面PAB⊥平面PBC也不成立；BC∥AD∥平面PAD，
∴直线BC∥平面PAE也不成立．
∵PA=$\sqrt{3}$AB，PA⊥平面ABC
∴PF=PB，BF=$\sqrt{3}$AB
∴△PFB为等边三角形，
故选：D．

点评 本题考查直线与平面成的角、直线与平面垂直的性质，属于基础题．

练习册系列答案
相关题目
2．在△ABC中，|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{AB}$-$\overrightarrow{AC}$|，AC=1，BC=$\sqrt{3}$，M是边BC上靠近C的一个四等分点，若N是BC边上的动点，则$\overrightarrow{AM}$•$\overrightarrow{AN}$的取值范围是[$\frac{1}{2}$，$\frac{3}{4}$]．
10．设直线y=kx与椭圆$\frac{x^2}{2}+{y^2}=1$相交于A，B两点，分别过A，B向x轴作垂线，若垂足恰为椭圆的两个焦点，则k=（　　）
A．±1B．$±\frac{{\sqrt{2}}}{2}$C．$±\frac{1}{2}$D．$±\frac{1}{4}$
7．如图所示，AE，DF是圆柱的两条母线，过AD作圆柱的截面交下底面于BC，且AD=BC，圆柱的高为2，底面半径为$\sqrt{3}$
（Ⅰ）求证：平面AEB∥平面DFC
（Ⅱ）求证：BC⊥AB
（Ⅲ）求四棱锥E-ABCD体积最大时AD的值．
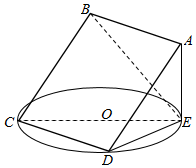14．如图所示，正方形ABCD所在平面与圆O所在平面相交于CD，线段CD为圆O的弦，AE垂直于圆O所在平面，垂足E是圆O上异于C，D的点，AE=3，圆O的直径为9．
（Ⅰ）求证：平面ABCD⊥平面ADE； 
（Ⅱ）求三棱锥D-ABE的体积．
4．已知函数F（x）=（$\frac{lnx}{x}$）2+（a-1）$\frac{lnx}{x}$+1-a有三个不同的零点x1，x2，x3（其中x1＜x2＜x3），则（1-$\frac{ln{x}_{1}}{{x}_{1}}$）2（1-$\frac{ln{x}_{2}}{{x}_{2}}$）（1-$\frac{ln{x}_{3}}{{x}_{3}}$）的值为（　　）
A．1-aB．a-1C．-1D．1
11．若不等式x2+ax+1≥0对于一切x∈（0，$\frac{1}{2}$）恒成立，则a的取值范围是（　　）
A．a≥0B．a≥-2C．a≥-$\frac{5}{2}$D．a≥-3
8．已知A={x|-x2+3x-2＞0}，B={x|x2-（a+1）x-a≤0}．
（1）化简集合B；
（2）若A⊆B，求实数a的取值范围．
9．若{bn}满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x-y≤0}\\{x+y-4≤0}\end{array}\right.$，则z=x+2y的最小值为（　　）
A．3B．4C．7D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网