题目内容
7.已知数列{an}的前n项和Sn满足Sn=a(Sn-an+1)(a为常数,且a>0),且4a3是a1与2a2的等差中项.(1)求{an}的通项公式;
(2)设bn=$\frac{2n+1}{{a}_{n}}$,求数列{bn}的前n项和Tn.
分析 (1)由4a3是a1与2a2的等差中项,可得2×4a3=a1+2a2.利用Sn=a(Sn-an+1),分别取n=1,2,3,可得a1,a2,a3,代入解得a.再利用递推关系即可得出an.
(2)bn=$\frac{2n+1}{{a}_{n}}$=(2n+1)•2n,利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)∵4a3是a1与2a2的等差中项,∴2×4a3=a1+2a2.
∵Sn=a(Sn-an+1),∴a1=a(a1-a1+1),a1+a2=a(a1+a2-a2+1),a1+a2+a3=a(a1+a2+a3-a3+1),
解得a1=a,a2=a2,a3=a3,
∴8a3=a+2a2,a>0,
化为8a2-2a-1=0,
解得a=$\frac{1}{2}$.
∴Sn=$\frac{1}{2}$(Sn-an+1),
化为Sn=1-an,
当n≥2时,an=Sn-Sn-1=1-an-(1-an-1),
化为$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{1}{2}$,
∴数列{an}是等比数列,首项与公比都为$\frac{1}{2}$.
∴an=$(\frac{1}{2})^{n}$.
(2)bn=$\frac{2n+1}{{a}_{n}}$=(2n+1)•2n,
∴数列{bn}的前n项和Tn=3×2+5×22+7×23+…+(2n+1)•2n,
2Tn=3×22+5×23+…+(2n-1)•2n+(2n+1)•2n+1,
∴-Tn=3×2+2(22+23+…+2n)-(2n+1)•2n+1=2+2×$\frac{2({2}^{n}-1)}{2-1}$-(2n+1)•2n+1=-2-(1-2n)•2n+1,
∴Tn=2+(2n-1)•2n+1.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、递推关系、“错位相减法”,考查了推理能力与计算能力,属于中档题.

| A. | [-$\frac{2}{3}$,$\frac{1}{3}$] | B. | [$\frac{1}{3}$,$\frac{4}{3}$] | C. | [-$\frac{1}{6}$,$\frac{5}{6}$] | D. | [$\frac{5}{6}$,$\frac{11}{6}$] |
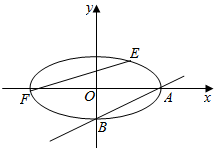 已知椭圆线$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,如图所示,A(a,0),B(0,-b)原点到直线AB的距离为$\frac{4}{\sqrt{5}}$.
已知椭圆线$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,如图所示,A(a,0),B(0,-b)原点到直线AB的距离为$\frac{4}{\sqrt{5}}$.