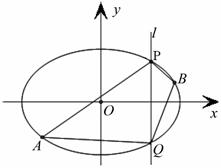
题目内容
如图所示,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.
(1)求x1x2与y1y2的值;
(2)求证:OM⊥ON.
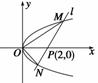
(1)解 过点P(2,0)且斜率为k的直线方程为:y=k(x-2).
把y=k(x-2)代入y2=2x,
消去y得k2x2-(4k2+2)x+4k2=0,
由于直线与抛物线交于不同两点,
故k2≠0且Δ=(4k2+2)2-16k4=16k2+4>0,
x1x2=4,x1+x2=4+ ,
,
∵M、N两点在抛物线上,
∴y ·y
·y =4x1·x2=16,
=4x1·x2=16,
而y1·y2<0,∴y1y2=-4.


练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 ≠1,设命题p:函数y=cx在R上单调递减,命题q:不等式x2-
≠1,设命题p:函数y=cx在R上单调递减,命题q:不等式x2-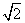 x+c>0的解集为R.如果命题“p∨q”为真命题,“p∧q”为假命题,求实数c的取值范围.
x+c>0的解集为R.如果命题“p∨q”为真命题,“p∧q”为假命题,求实数c的取值范围. 与直线y=k(x-2)+4有两个交点时,实数k的取值范围是__________.
与直线y=k(x-2)+4有两个交点时,实数k的取值范围是__________.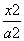 +y2=1 (a>1)短轴的一个端点,Q为椭圆上的一个动点,求PQ的最大值.
+y2=1 (a>1)短轴的一个端点,Q为椭圆上的一个动点,求PQ的最大值. |
| -2x-3
-2x-3 ﹜,则A
﹜,则A B=( )
B=( ) B.{3} C.{0} D.{-2}
B.{3} C.{0} D.{-2} 在点(0,1)处的切线方程为( )
在点(0,1)处的切线方程为( ) 等于
等于 B.
B. C.
C. D.
D.
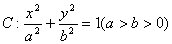 的离心率为
的离心率为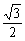 ,长轴长为
,长轴长为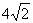 .
.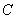 的方程;
的方程;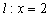 与椭圆
与椭圆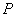 、
、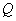 ,其中
,其中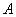 、
、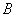 是椭圆上位于直线
是椭圆上位于直线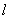 两侧的两个动点,满足
两侧的两个动点,满足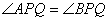 ,试问直线
,试问直线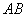 的斜率是否为定值?请说明理由.
的斜率是否为定值?请说明理由.