题目内容
已知c>0，c
≠1，设命题p：函数y＝cx在R上单调递减，命题q：不等式x2－
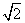x＋c>0的解集为R.如果命题“p∨q”为真命题，“p∧q”为假命题，求实数c的取值范围．
解 ∵y＝cx在R上单调递减，
∴0<c<1，命题p：0<c<1.
∵不等式x2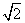－x＋c>0的解集为R，
∴Δ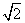＝(－)2－4c<0，c>
，
∴命题q：c>.
∵“p∨q”为真命题，“p∧q”为假命题，
∴命题p与命题q恰好一真一假，
∴p为真q为假，或p为假q为真，
，解得
0<c≤或c≥1.
综上可知，实数c的取值范围是(1，]∪[1，＋∞)．
练习册系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
___________________________.
B的________条件．
_条件．
，焦点是(－3,0)，(3,0)，则椭圆方程为
______________．