题目内容
设P是椭圆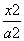
＋y2＝1 (a>1)短轴的一个端点，Q为椭圆上的一个动点，求PQ的最大值．
解 依题意可设P(0,1)，Q(x，y)，
则PQ＝
，又因为Q在椭圆上，
所以，x2＝a2(1－y2)，
PQ2＝a2(1－y2)＋y2－2y＋1
＝(1－a2)y2－2y＋1＋a2
练习册系列答案
小题狂做系列答案
相关题目
小题狂做系列答案题目内容
设P是椭圆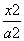＋y2＝1 (a>1)短轴的一个端点，Q为椭圆上的一个动点，求PQ的最大值．
解 依题意可设P(0,1)，Q(x，y)，
则PQ＝，又因为Q在椭圆上，
所以，x2＝a2(1－y2)，
PQ2＝a2(1－y2)＋y2－2y＋1
＝(1－a2)y2－2y＋1＋a2
小题狂做系列答案
－
＝1 (a>0，b>0)有相同的焦点F，点A是两曲线的交点，且AF⊥x轴，则双曲线的离心率为________．
－y2＝1的两个焦点，点P在双曲线上，∠F1PF2＝90°，则△F1PF2的面积是________．
＝1 (a>b>0)的焦点为F1，F2，两条准线与x轴的交点分别为M，N，若MN≤2F1F2，则该椭圆离心率的取值范围是________．
在
处导数存在，若p：
；q：x=x0是
是
的充分必要条件
的单调区间； 
处取得极值，直线y=m与
的图象有三个不同的交点，求m的取值范围。
上一点
到其焦点
的距离为4，则
(
为原点)的面积为_____________．