题目内容
10．若抛物线y2=2px的准线经过双曲线x2-y2=2的右焦点，则p的值为（ ）| A． | -2 | B． | -3 | C． | -4 | D． | -5 |
分析 先求出双曲线x2-y2=2的右焦点，得到抛物线y2=2px的准线，依据p的意义求出它的值．
解答 解：双曲线x2-y2=2的右焦点为（2，0），故抛物线y2=2px的准线为x=2，
∴-$\frac{p}{2}$=2，∴p=-4，
故选C．
点评 本题考查抛物线和双曲线的简单性质，以及抛物线方程y2=2px中p的意义．
练习册系列答案
相关题目
2．设函数f'（x）是函数f（x）（x∈R）的导函数，f（0）=1，且$f（x）=\frac{1}{3}f'（x）-1$，则4f（x）＞f'（x）的解集为（ ）
| A． | $（\frac{ln4}{3}，+∞）$ | B． | $（\frac{ln2}{3}，+∞）$ | C． | $（\frac{{\sqrt{3}}}{2}，+∞）$ | D． | $（\frac{{\sqrt{e}}}{3}，+∞）$ |
19．已知双曲线方程为$\frac{x^2}{{{m^2}+4}}-\frac{y^2}{b^2}=1$，若其过焦点的最短弦长为2，则该双曲线的离心率的取值范围是（ ）
| A． | $（1，\frac{{\sqrt{6}}}{2}]$ | B． | $[\frac{{\sqrt{6}}}{2}，+∞）$ | C． | $（1，\frac{{\sqrt{6}}}{2}）$ | D． | $（\frac{{\sqrt{6}}}{2}，+∞）$ |
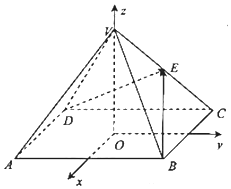如图，以正四棱锥V-ABCD的底面中心O为坐标原点建立空间直角坐标系O-xyz，其中Ox∥BC，Oy∥AB，E为VC中点，正四棱锥的底面边长为2a，高为h，且有cos＜$\overrightarrow{BE}$，$\overrightarrow{DE}$＞=-$\frac{15}{49}$．