题目内容
5.如表是x与y之间的一组数据,则y关于x的回归方程$\stackrel{∧}{y}$=bx+$\stackrel{∧}{a}$必过点(1.5,4).| x | 0 | 1 | 2 | 3 |
| y | 1 | 2.5 | 5.5 | 7 |
分析 根据回归方程$\stackrel{∧}{y}$=bx+$\stackrel{∧}{a}$必过样本中心点,求出$\overline{x}$、$\overline{y}$即可.
解答 解:根据表中数据,计算
$\overline{x}$=$\frac{1}{4}$×(0+1+2+3)=1.5,
$\overline{y}$=$\frac{1}{4}$×(1+2.5+5.5+7)=4;
所以y关于x的回归方程$\stackrel{∧}{y}$=bx+$\stackrel{∧}{a}$必过样本中心点(1.5,4).
故答案为:(1.5,4).
点评 本题考查了线性回归方程必过样本中心点的应用问题,是基础题目.

练习册系列答案
相关题目
16.设a,b,c∈R,且a>b,则( )
| A. | ac>bc | B. | a-c<b-c | C. | a2>b2 | D. | a3>b3 |
20.设集合A={(x,y)|(x-4)2+y2=1},B={(x,y)|(x-t)2+(y-at+2)2=1},如果命题“?t∈R,A∩B=∅”是真命题,则实数a的取值范围是( )
| A. | (-∞,0)∪($\frac{4}{3}$,+∞) | B. | (0,$\frac{4}{3}$] | C. | [0,$\frac{4}{3}$] | D. | (-∞,0]∪[$\frac{4}{3}$,+∞) |
10.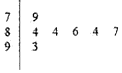 如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是( )
如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是( )
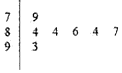 如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是( )
如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是( )| A. | 85.84 | B. | 84.85 | C. | 85.87 | D. | 84.86 |
17.已知{an}是等差数列,a1=-26,a8+a13=5,当{an}的前n项和Sn取最小值时,n等于( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
14.已知a>1,$x={log_a}\sqrt{2}+\frac{1}{2}{log_a}3$,$y=\frac{1}{2}{log_a}5$,$z={log_a}\sqrt{21}-{log_a}\sqrt{3}$,则( )
| A. | x>y>z | B. | z>y>x | C. | y>x>z | D. | z>x>y |
15.用二分法找函数f(x)=2x+3x-7在区间[0,4]上的零点近似值,取区间中点2,则下一个存在零点的区间为( )
| A. | (0,1) | B. | (0,2) | C. | (2,3) | D. | (2,4) |