题目内容
8．设f（x）为定义在R上的奇函数，f（1）=1，f（x+2）=f（x）+f（2），则f（5）=5．分析 利用奇函数求出f（0），利用抽象函数求出f（2），转化求解f（5）即可．
解答 解：f（x）为定义在R上的奇函数，可得f（0）=0；
f（1）=1，f（x+2）=f（x）+f（2），
当x=1时，f（3）=f（1）+f（2）=1+f（2），
当x=-1时，f（1）=f（-1）+f（2），可得f（2）=2．
f（5）=f（3）+f（2）=1+2f（2）=1+4=5．
故答案为：5．
点评 本题考查抽象函数的应用，函数值的求法，赋值法的应用，考查计算能力．
练习册系列答案
相关题目
18．已知集合A={-1，0，1}，B={1，2}，则A∪B等于（ ）
| A． | {0，1} | B． | {1} | C． | {-1，0，1，2} | D． | {1，2} |
1．在△ABC中，角A．B、C的对边分别为a，b，c，若2a=3b，则$\frac{9si{n}^{2}B-si{n}^{2}A}{si{n}^{2}A}$=（ ）
| A． | 2 | B． | 3 | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
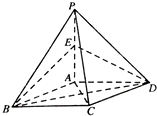如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，且PA⊥底面ABCD，BD⊥PC，E是PA的中点，∠BAD=120°．