Question

已知函数f（x）=3^x，f（a+2）=27，函数g（x）=λ•2^ax-4^x的定义域为[0，2]，讨论方程g（x）=λ+1的解的个数．

Answer 1

考点：函数与方程的综合运用

专题：函数的性质及应用

分析：利用已知条件求出a，然后利用化简g（x）=λ+1，得到λ的关系式，通过函数的定义域求出表达式的最值即可．

解答： 解：∵f（x）=3^x，∴f（a+2）=27，即3^a+2=27，解得a=1，
∴函数g（x）=λ•2^ax-4^x=λ•2^x-4^x，
g（x）=λ+1=λ•2^x-4^x，x∈[0，2]，2^x∈[1，4]
当x≠0时，可得λ=

1+4x

2x-1

=2x+1+

2

2x-1

=2x-1+

2

2x-1

+2≥2+2

2

，当且仅当2x-1=

2

2x-1

，时λ取得最小值．
x=2时，λ=

17

3

．
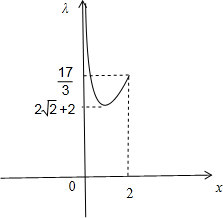
函数λ=

1+4x

2x-1

，x∈[0，2]，的图象为：
当

17

3

≥λ≥log2(1+

2

)，g（x）=λ+1的解的个数为2个．
当λ＞

17

3

时，g（x）=λ+1的解的个数为一个．

点评：本题综合考查了函数的性质，函数的交点，方程的根的问题，运用图象，单调性解决即可，综合性较大．