题目内容
画出下列函数的图象,并写出它们的定义域、值域、单调区间、最大最小值.
(1)y=x+1;
(2)y=x2-|x|-3;
(3)y=
;
(4)y=|x-2|+|x+1|.
(1)y=x+1;
(2)y=x2-|x|-3;
(3)y=
| x2-1 |
| x+1 |
(4)y=|x-2|+|x+1|.
考点:函数的值域,函数的定义域及其求法
专题:函数的性质及应用
分析:分别画出函数的图象,并根据图象写出它们的定义域、值域、单调区间、最大最小值.
解答:
解:(1)y=x+1的定义域R、值域R、单调区间(-∞,+∞)、无最大值,无最小值.
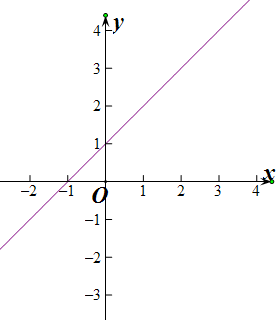
(2)y=x2-|x|-3的定义域R、
f(
)=-
,值域[-
,+∞)
、单调递减区间(-∞,-
)(0,
)、单调递增区间(-
,0),(
,+∞);
无最大值,最小值为-
.

(3)y=
的定义域(-∞,-1)∪(-1,+∞)、值域为(-∞,0)∪(0,+∞)、
、单调递增区间(-∞,-1),(-1,+∞)、最大最小值.
y=
=x-1,x≠1,
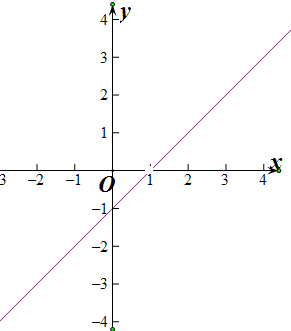
(4)∵f(-1)=3,f(2)=3,
∴y=|x-2|+|x+1|的定义域为R、值域[3,+∞)、单调递减区间(-∞,-1),单调递增区间(2,+∞)、无最大值,最小值为3.
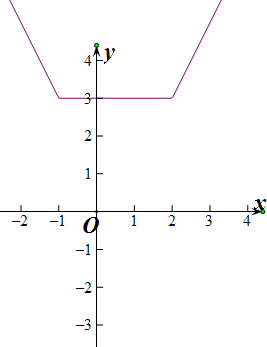
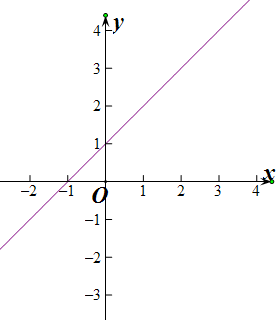
(2)y=x2-|x|-3的定义域R、
f(
| 1 |
| 2 |
| 13 |
| 4 |
| 13 |
| 4 |
、单调递减区间(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
无最大值,最小值为-
| 13 |
| 4 |

(3)y=
| x2-1 |
| x+1 |
、单调递增区间(-∞,-1),(-1,+∞)、最大最小值.
y=
| x2-1 |
| x+1 |
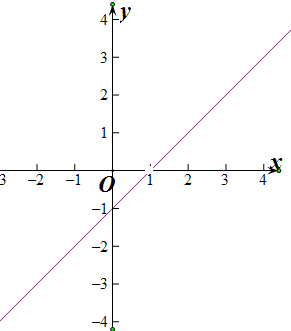
(4)∵f(-1)=3,f(2)=3,
∴y=|x-2|+|x+1|的定义域为R、值域[3,+∞)、单调递减区间(-∞,-1),单调递增区间(2,+∞)、无最大值,最小值为3.
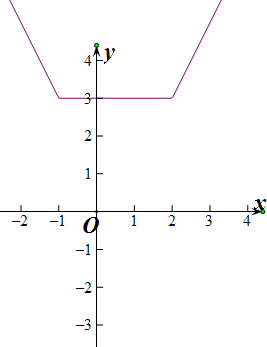
点评:本题考查了运用函数的图象解决函数的性质,属于数形结合的思想的运用,属于容易题,

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(∁UA)∪B为( )
| A、{1,2,4} |
| B、{2,3,4} |
| C、{0,2,3,4} |
| D、{0,2,4} |
如果
(1-2x)n存在,那么x的取值范围是( )
| lim |
| n→∞ |
| A、0≤x<1 |
| B、0<x<1 |
| C、0≤x≤1 |
| D、0<x≤1 |