题目内容
8.已知△ABC中,角A,B,C所对的边分别为a,b,c,且△ABC的面积S=2$\sqrt{3}$,b=$\sqrt{7}$a,B=120°.(1)求b、c的值;
(2)证明:tanA=$\frac{S}{10}$.
分析 (1)由△ABC的面积S=2$\sqrt{3}$,b=$\sqrt{7}$a,B=120°.可得2$\sqrt{3}$=$\frac{1}{2}ac$sin120°,$b=\sqrt{7}$a,b2=a2+c2-
2accos120°,联立解出即可得出.
(2)利用正弦定理、同角三角函数基本关系式即可得出.
解答 解:(1)∵△ABC的面积S=2$\sqrt{3}$,b=$\sqrt{7}$a,B=120°.
∴2$\sqrt{3}$=$\frac{1}{2}ac$sin120°,$b=\sqrt{7}$a,b2=a2+c2-2accos120°,
解得a=2,b=2$\sqrt{7}$,c=4.
(2)证明:由(1)可得:$\frac{2}{sinA}$=$\frac{2\sqrt{7}}{sin12{0}^{°}}$,解得sinA=$\frac{\sqrt{21}}{14}$.
∵a<b,∴A为锐角,
∴cosA=$\frac{5\sqrt{7}}{14}$.
∴tanA=$\frac{sinA}{cosA}$=$\frac{\sqrt{3}}{5}$=$\frac{2\sqrt{3}}{10}$=$\frac{S}{10}$.
即tanA=$\frac{S}{10}$.
点评 本题考查了正弦定理余弦定理、三角函数求值、三角形面积计算公式、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.已知抛物线y2=8x的准线与双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{16}$=1相交于A,B两点,点F为抛物线的焦点,△ABF为直角三角形,则双曲线的离心率为( )
| A. | 3 | B. | $\sqrt{2}+1$ | C. | 2 | D. | $\sqrt{3}$ |
16.已知集合M={x|x2+x-2=0,x∈R},N={x|x<0,x∈R},则M∩N=( )
| A. | ϕ | B. | {1} | C. | {-2} | D. | {-2,1} |
13.函数x=1在y=2x3-x2+1出的导数值为( )
| A. | 3 | B. | 2 | C. | 5 | D. | 4 |
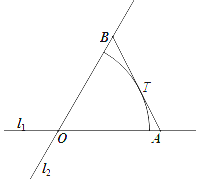 如图,在某商业区周边有两条公路l1和l2,在点O处交汇;该商业区为圆心角$\frac{π}{3}$、半径3km的扇形.现规划在该商业区外修建一条公路AB,与l1,l2分别交于A,B,要求AB与扇形弧相切,切点T不在l1,l2上.
如图,在某商业区周边有两条公路l1和l2,在点O处交汇;该商业区为圆心角$\frac{π}{3}$、半径3km的扇形.现规划在该商业区外修建一条公路AB,与l1,l2分别交于A,B,要求AB与扇形弧相切,切点T不在l1,l2上.