题目内容
1.已知圆C的方程为(x-1)2+y2=1,P是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上一点,过P作圆的两条切线,切点为A,B,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围为( )| A. | [$\frac{3}{2}$,+∞) | B. | [2$\sqrt{2}$-3,+∞) | C. | [2$\sqrt{2}$-3,$\frac{56}{9}$] | D. | [$\frac{3}{2}$,$\frac{56}{9}$] |
分析 利用圆切线的性质:与圆心切点连线垂直;设出一个角,通过解直角三角形求出PA,PB的长;利用向量的数量积公式表示出$\overrightarrow{PA}$•$\overrightarrow{PB}$,利用三角函数的二倍角公式化简函数,通过换元,再利用基本不等式求出最值.
解答 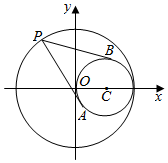 解:设PA与PB的夹角为2α,
解:设PA与PB的夹角为2α,
则|PA|=PB|=$\frac{1}{tanα}$,
∴y=$\overrightarrow{PA}$•$\overrightarrow{PB}$=|PA||PB|cos2α=$\frac{1}{ta{n}^{2}α}$•cos2α
=$\frac{1+cos2α}{1-cos2α}$•cos2α.
记cos2α=u,则y=$\frac{u(u+1)}{1-u}$=-3+(1-u)+$\frac{2}{1-u}$≥2$\sqrt{2}$-3,
∵P在椭圆的左顶点时,sinα=$\frac{1}{3}$,∴cos2α=$\frac{7}{9}$,
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$的最大值为$\frac{1+\frac{7}{9}}{1-\frac{7}{9}}$•$\frac{7}{9}$=$\frac{56}{9}$,
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$的范围为[2$\sqrt{2}$-3,$\frac{56}{9}$].
故选:C.
点评 本题考查圆的切线的性质、三角函数的二倍角公式、向量的数量积公式、基本不等式求函数的最值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在区间[-3,3]上随机取一个数x,使得|x+1|-|x-2|≥1成立的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
9.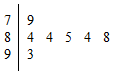 如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
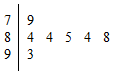 如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 84,4.84 | B. | 84,1.6 | C. | 85,2.4 | D. | 85,1.6 |
16.复数(2+i)(1-i)等于( )
| A. | 1-i | B. | 2-i | C. | 3+i | D. | 3-i |
 (重点中学做)已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,1),离心率e=$\frac{\sqrt{6}}{3}$
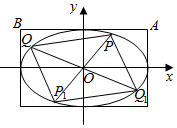
(重点中学做)已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,1),离心率e=$\frac{\sqrt{6}}{3}$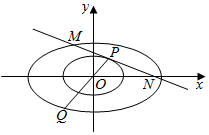 如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点A(0,$\sqrt{3}$)和点P都在椭圆C1上,椭圆C2方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=4.
如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点A(0,$\sqrt{3}$)和点P都在椭圆C1上,椭圆C2方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=4.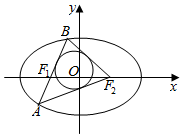 如图,设椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左右焦点分别为F1、F2,过焦点F1的直线交椭圆于A、B两点,若以△ABF2的内切圆的面积为π,设A(x1,y1)、B((x2,y2),则|y1-y2|值为$\frac{10}{3}$.
如图,设椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左右焦点分别为F1、F2,过焦点F1的直线交椭圆于A、B两点,若以△ABF2的内切圆的面积为π,设A(x1,y1)、B((x2,y2),则|y1-y2|值为$\frac{10}{3}$.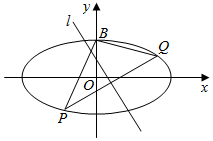 已知中心在原点O,焦点在x轴上的椭圆的一个顶点为B(0,1),B到焦点的距离为2.
已知中心在原点O,焦点在x轴上的椭圆的一个顶点为B(0,1),B到焦点的距离为2.