题目内容

1．已知f（x）=lo${g}_{{a}^{2}}$（x-1）在（1，+∞）是减函数，那么a的取值范围是0＜a＜1或-1＜a＜0．

分析 根据复合函数单调性的性质进行求解即可．

解答 解：∵f（x）=lo${g}_{{a}^{2}}$（x-1）在（1，+∞）是减函数，
∴函数y=lo${g}_{{a}^{2}}$t为减函数，
则0＜a2＜1，得0＜a＜1或-1＜a＜0，
故实数a的取值范围是0＜a＜1或-1＜a＜0，
故答案为：0＜a＜1或-1＜a＜0．

点评 本题主要考查函数单调性的应用，结合复合函数单调性的关系是解决本题的关键．

练习册系列答案
相关题目
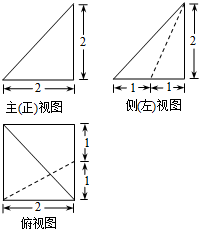11．已知四棱锥的三视图（如图所示），则该四棱锥的体积为2，在该四棱锥的四个侧面中，面积最小的侧面面积是1．
12．设随机变量X具有分布P（X=k）=$\frac{1}{5}$，k=1，2，3，4，5，求E（X+2）2，D（2X-1），$\sqrt{D（X-1）}$．
9．已知函数f（x）=3sin（$\frac{x}{2}$+$\frac{π}{4}$）+3．
（1）用五点法画出它在一个周期内的闭区间上的图象；
（2）若α为第二象限角，且f（2α-π）=3+2$\sqrt{2}$，求$\frac{cosαcos2α}{1+cos2α+sin2α}$的值．
16．已知（x-$\frac{1}{\sqrt{11}}$）n展开式的第3项系数为6，求n的值．
6．lo${g}_{{a}^{2}}$b•logb$\sqrt{a}$的值等于$\frac{1}{4}$．
13．化简：$\frac{cos（α-π）tan（α-2π）tan（2π-α）}{sin（π+α）}$．
10．直径为20cm的圆中，弧长为5cm的圆弧所对圆心角为$\frac{1}{2}$．
11．某班要选举班级干部，现有10名候选人，要从10名候选人中选出5人．
（1）将这5人组成班委，有多少种不同的选法？
（2）让这5人担任班委中五项不同的职务，有多少种不同的选法？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网