题目内容
11.$sin\frac{7π}{8}cos\frac{7π}{8}$=$-\frac{{\sqrt{2}}}{4}$.分析 利用二倍角公式和诱导公式求解.
解答 解:由$sin\frac{7π}{8}cos\frac{7π}{8}$=$\frac{1}{2}$sin(2×$\frac{7π}{8}$)=$\frac{1}{2}$sin$\frac{7π}{4}$=$\frac{1}{2}$sin(2π$-\frac{π}{4}$)=-$\frac{1}{2}$sin$\frac{π}{4}$=$-\frac{\sqrt{2}}{4}$
故答案为$-\frac{{\sqrt{2}}}{4}$.
点评 本题主要考察了二倍角公式的诱导公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
15.函数y=log${\;}_{\frac{1}{2}}$(x2-3x+2)的单调递增区间为是( )
| A. | (0,+∞) | B. | (-∞,1) | C. | (-∞,$\frac{3}{2}$] | D. | (2,+∞) |
16.sin2010°的值等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
3.设函数f(x)=$\frac{{4}^{x}}{{4}^{x}+1}$,若[x]表示不超过x的最大整数,则函数y=[f(x)-$\frac{1}{2}$]+[f(x)+$\frac{1}{2}$]的值域是( )
| A. | {0,-1} | B. | {0,1} | C. | {-1,1} | D. | {-1,0,1} |
1.若a=log23,b=2.11.1,c=lg2+lg5,则a,b,c的大小关系为( )
| A. | b>a>c | B. | a>b>c | C. | c>b>a | D. | 无法确定 |
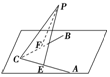 ∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2$\sqrt{3}$ cm,那么PC与平面ABC所成角的大小为45°.
∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2$\sqrt{3}$ cm,那么PC与平面ABC所成角的大小为45°.