题目内容
如图,椭圆 的左顶点、右焦点分别为A,F,直线l的方程为x=9,N为l上一点,且在x轴的上方,AN与椭圆交于M点
的左顶点、右焦点分别为A,F,直线l的方程为x=9,N为l上一点,且在x轴的上方,AN与椭圆交于M点(1)若M是AN的中点,求证:MA⊥MF.
(2)过A,F,N三点的圆与y轴交于P,Q两点,求|PQ|的范围.

【答案】分析:(1)欲证MA⊥MF,只需证明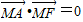 ,分别求出
,分别求出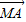 ,
,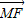 的坐标,再用向量的数量积的坐标运算计算即可.
的坐标,再用向量的数量积的坐标运算计算即可.
(2)欲求|PQ|的范围,需先将|PQ|用某个参数表示,再求最值,可先找到圆心坐标和半径,再利用圆中半径,半弦,弦心距组成的直角三角形,得到用参数表示的|PQ|,再用均值不等式求范围.
解答:解:(1)由题意得A(-6,0),F(4,0),xN=9∴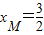
又M点在椭圆上,且在x轴上方,得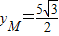
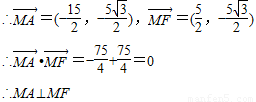
(2)设N(9,t),其中t>0,∵圆过A,F,N三点,
∴设该圆的方程为x2+y2+Dx+Ey+F=0,有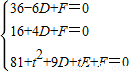
解得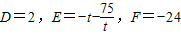
∴圆心为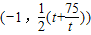 ,半径r=
,半径r=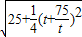
∴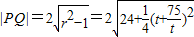 ,
,
∵t>0∴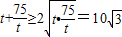 ,当且仅当
,当且仅当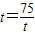 ,即
,即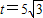 时取“=”
时取“=”
∴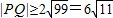 ,∴|PQ|的取值范围是
,∴|PQ|的取值范围是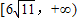
点评:本题考查了椭圆与圆之间的关系,其中圆中弦长的求法必须掌握.
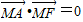 ,分别求出
,分别求出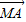 ,
,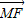 的坐标,再用向量的数量积的坐标运算计算即可.
的坐标,再用向量的数量积的坐标运算计算即可.(2)欲求|PQ|的范围,需先将|PQ|用某个参数表示,再求最值,可先找到圆心坐标和半径,再利用圆中半径,半弦,弦心距组成的直角三角形,得到用参数表示的|PQ|,再用均值不等式求范围.
解答:解:(1)由题意得A(-6,0),F(4,0),xN=9∴
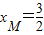
又M点在椭圆上,且在x轴上方,得
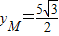
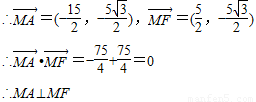
(2)设N(9,t),其中t>0,∵圆过A,F,N三点,
∴设该圆的方程为x2+y2+Dx+Ey+F=0,有
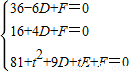
解得
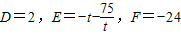
∴圆心为
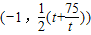 ,半径r=
,半径r=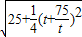
∴
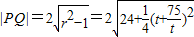 ,
,∵t>0∴
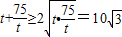 ,当且仅当
,当且仅当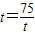 ,即
,即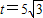 时取“=”
时取“=”∴
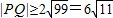 ,∴|PQ|的取值范围是
,∴|PQ|的取值范围是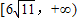
点评:本题考查了椭圆与圆之间的关系,其中圆中弦长的求法必须掌握.

练习册系列答案
相关题目

 的左顶点为
的左顶点为 ,
, 是椭圆
是椭圆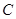 上异于点
上异于点 与点
与点
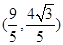 ,求
,求 的值;
的值;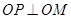 ,求
,求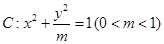 的左顶点为
的左顶点为 ,
,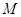 是椭圆
是椭圆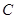 上异于点
上异于点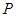 与点
与点 ,求
,求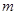 的值;
的值;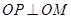 ,求
,求
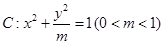 的左顶点为
的左顶点为 ,
,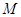 是椭圆
是椭圆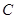 上异于点
上异于点 与点
与点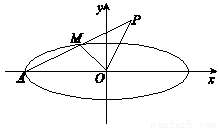
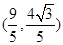 ,求
,求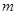 的值;
的值;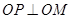 ,求
,求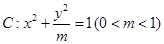 的左顶点为
的左顶点为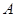 ,
, 是椭圆
是椭圆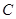 上异于点
上异于点 与点
与点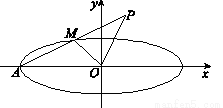
 ,求
,求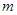 的值;
的值;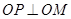 ,求
,求