题目内容
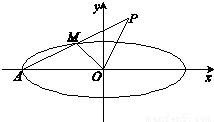
如图,椭圆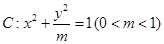 的左顶点为
的左顶点为 ,
,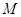 是椭圆
是椭圆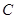 上异于点
上异于点 的任意一点,点
的任意一点,点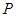 与点
与点 关于点
关于点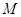 对称.
对称.
(Ⅰ)若点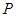 的坐标为
的坐标为 ,求
,求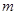 的值;
的值;
(Ⅱ)若椭圆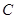 上存在点
上存在点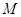 ,使得
,使得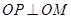 ,求
,求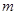 的取值范围.
的取值范围.

【答案】
(I)  ;(II)
;(II)  .
.
【解析】
试题分析:(I)利用中点坐标公式,求M坐标,代入椭圆方程即可求m;(II)设 ,表示出P坐标,再利用垂直条件写关系式,求
,表示出P坐标,再利用垂直条件写关系式,求 的取值范围.
的取值范围.
试题解析:(Ⅰ)解:依题意, 是线段
是线段 的中点,
的中点,

因为 ,
, ,
,
所以 点 的坐标为
的坐标为 .2分
.2分
由点 在椭圆
在椭圆 上,
上,
所以  ,
4分
,
4分
解得  .
5分
.
5分
(Ⅱ)解:设 ,则
,则
 ,且
,且 . ① 6分
. ① 6分
因为  是线段
是线段 的中点,
的中点,
所以  .
7分
.
7分
因为  ,
,
所以  . ②
8分
. ②
8分
由 ①,②
消去 ,整理得
,整理得
 .
10分
.
10分
所以  ,
12分
,
12分
当且仅当  时,上式等号成立.
时,上式等号成立.
所以  的取值范围是
的取值范围是 .
13分
.
13分
考点:1.中点坐标公式;2.基本不等式,分离常数;3.转化思想.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 的左顶点为
的左顶点为 ,
, 是椭圆
是椭圆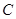 上异于点
上异于点 与点
与点
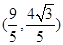 ,求
,求 的值;
的值;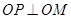 ,求
,求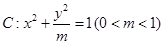 的左顶点为
的左顶点为 ,
,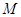 是椭圆
是椭圆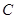 上异于点
上异于点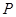 与点
与点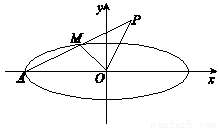
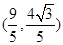 ,求
,求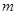 的值;
的值;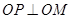 ,求
,求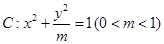 的左顶点为
的左顶点为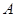 ,
, 是椭圆
是椭圆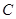 上异于点
上异于点 与点
与点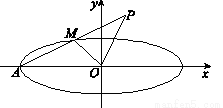
 ,求
,求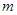 的值;
的值;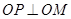 ,求
,求 的左顶点为A,M是椭圆C上异于点A的任意一点,点P与点A关于点M对称.
的左顶点为A,M是椭圆C上异于点A的任意一点,点P与点A关于点M对称. ,求m的值;
,求m的值;