题目内容
若函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[-1,1]时,f(x)=x2,那么函数y=f(x)的图象与函数g(x)=
的图象在(-12,12)内交点的个数为( )
|
| A、18 | B、20 | C、21 | D、22 |
考点:根的存在性及根的个数判断
专题:计算题,作图题,函数的性质及应用
分析:由题意,画出函数f(x)与g(x)=
在(-12,12)内的图象,由图象解答.
|
解答:
解:因为f(x+2)=f(x),
所以f(x)的周期为2,
在x∈[-1,1]时,f(x)=x2,
画出函数f(x)与g(x)=
在(-12,12)内的图象,
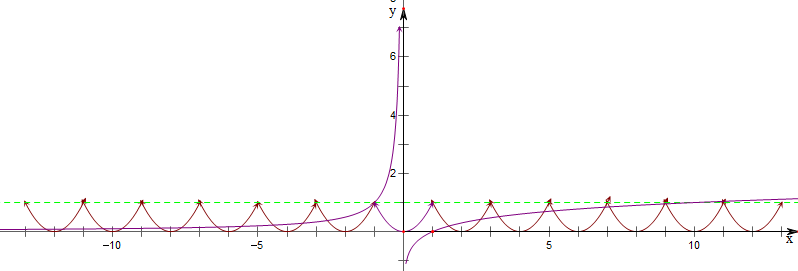
发现f(x)=x2在x轴右侧的图象与g(x)=lg x有9个交点,
f(x)=x2在x轴左侧的图象与g(x)=-
在(-12,0)内有11个交点,
一共有20个交点.
故选B.
所以f(x)的周期为2,
在x∈[-1,1]时,f(x)=x2,
画出函数f(x)与g(x)=
|

发现f(x)=x2在x轴右侧的图象与g(x)=lg x有9个交点,
f(x)=x2在x轴左侧的图象与g(x)=-
| 1 |
| x |
一共有20个交点.
故选B.
点评:本题考查了函数的零点,同时考查了学生的作图能力,属于中档题.

练习册系列答案
相关题目
在等差数列{an}中,若a4+a7=10,则{an}的前10项和为( )
| A、10 | B、20 | C、25 | D、50 |
已知函数f(x)=
则方程f(x)-a=0有四个实根的充要条件为( )
|
| A、a≥1 | B、a≤3 |
| C、1≤a≤3 | D、1<a<3 |
设函数f(x)=
(其中a>0且a≠1),若f(-
)=-
,则f-1(
)的值为( )
|
| 1 |
| 9 |
| 1 |
| 2 |
| 1 |
| 4 |
| A、1 | ||
B、
| ||
| C、3 | ||
D、
|
 如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是
如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是 如图,BA是⊙O的直径,AD是切线,BF、BD是割线,求证:BE•BF=BC•BD.
如图,BA是⊙O的直径,AD是切线,BF、BD是割线,求证:BE•BF=BC•BD.