Question

4．已知正方形ABCD，以A、C为焦点，且过B点的椭圆的离心率为（　　）

• A． $\sqrt{2}$
• B． $\frac{1+\sqrt{2}}{2}$
• C． $\frac{\sqrt{2}}{2}$
• D． $\frac{\sqrt{2}-1}{2}$

Answer 1

分析 如图所示，由正方形的性质可得：b=c，又a=$\sqrt{{b}^{2}+{c}^{2}}$，即可得出离心率．

解答 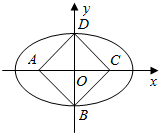解：如图所示，
由正方形的性质可得：b=c，
∴a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{2}$c．
∴椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$．
故选：C．

点评 本题考查了椭圆的标准方程及其性质、正方形的性质，考查了推理能力与计算能力，属于中档题．