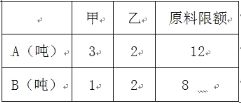
题目内容
【题目】在![]() 中,内角
中,内角![]() 的对边分别为
的对边分别为![]() ,已知
,已知![]() .
.
(1)求角![]() 的值;
的值;
(2)若![]() ,当
,当![]() 取最小值时,求
取最小值时,求![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:方法一:(Ⅰ)利用正弦定理、诱导公式、两角和的正弦公式化简已知的式子,由内角的范围和特殊角的三角函数值求出角C;(Ⅱ)利用余弦定理列出方程,由条件和完全平方公式化简后,利用基本不等式求出c的最小值,由面积公式求出△ABC的面积;方法二:(Ⅰ)利用余弦定理化简已知的式子得到边的关系,由余弦定理求出cosC的值,由内角的范围和特殊角的三角函数值求出角C;(Ⅱ)利用余弦定理列出方程,结合条件消元后,利用一元二次函数的性质求出c的最小值,由面积公式求出△ABC的面积
试题解析:解法一(1)∵![]() ,∴
,∴![]() ……………………1分
……………………1分
∴![]() ……………2分
……………2分
即 ![]() ……………3分
……………3分
∴![]() 4分
4分
∵![]() ∴
∴ ![]() …………5分
…………5分
又∵![]() 是三角形的内角,∴
是三角形的内角,∴![]() ……6分
……6分
(2)由余弦定理得:![]() …………7分
…………7分
∵ ![]() ,故
,故![]() 8分
8分
∴ ![]() (当且仅当
(当且仅当![]() 时等号成立) ………10分
时等号成立) ………10分
∴![]() 的最小值为2,故
的最小值为2,故![]() ……12分
……12分
解法二:(1)∵![]() ,∴
,∴ ![]() ………1分
………1分
∴ ![]() ,即
,即 ![]() …………3分
…………3分
∴ ![]() …5分
…5分
又∵![]() 是三角形的内角,∴
是三角形的内角,∴![]() 6分
6分
(2)由已知,![]() ,即
,即![]() ,故:
,故:
![]() ……………8分
……………8分
∴ ![]() …………10分
…………10分
∴当![]() 时,
时,![]() 的最小值为2,故
的最小值为2,故![]() …………12分
…………12分

练习册系列答案
相关题目