题目内容
6.已知f(x)=x($\frac{1}{{2}^{x}-1}$+$\frac{1}{2}$).(1)指出函数的奇偶性,并予以证明;
(2)求证:对任何x(x∈R,且x≠0)都有f(x)>0.
分析 (1)根据函数奇偶性的定义即可判定函数f(x)的奇偶性,并证明你的结论;
(2)根据指数函数的性质结合偶函数的对称性证明当x>0时,f(x)>0即可.
解答 证明:(1)f(x)=x($\frac{1}{{2}^{x}-1}$+$\frac{1}{2}$)=$\frac{x({2}^{x}-1)}{{2}^{x}+1}$.
则函数f(x)为偶函数.
∵f(-x)=$\frac{-x({2}^{-x}-1)}{{2}^{-x}+1}$=$\frac{-x•(1-{2}^{x})}{1+{2}^{x}}$=$\frac{x({2}^{x}-1)}{{2}^{x}+1}$=f(x),
∴函数f(x)为偶函数.
(2)∵函数f(x)为偶函数.
∴只要证明当x>0时,f(x)>0即可.
当x>0时,2x>1,则2x-1>0,2x+1>0,
则f(x)=$\frac{x({2}^{x}-1)}{{2}^{x}+1}$>0,
∴对所有非零实数x,都有f(x)>0成立.
点评 本题主要考查函数奇偶性的判断以及函数值的证明,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知lg2=a,1g7=b,则log1498=( )
| A. | $\frac{a-b}{a+b}$ | B. | $\frac{2a+b}{a+b}$ | C. | $\frac{a-2b}{a+b}$ | D. | $\frac{a+2b}{a+b}$ |
17.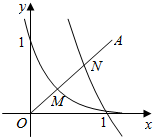 如图,点O为坐标原点,点A(1,1),若函数y=ax(a>0,且a≠1)及logbx(b>0,且b≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )
如图,点O为坐标原点,点A(1,1),若函数y=ax(a>0,且a≠1)及logbx(b>0,且b≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )
 如图,点O为坐标原点,点A(1,1),若函数y=ax(a>0,且a≠1)及logbx(b>0,且b≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )
如图,点O为坐标原点,点A(1,1),若函数y=ax(a>0,且a≠1)及logbx(b>0,且b≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )| A. | a<b<1 | B. | b<a<1 | C. | b>a>1 | D. | a>b>1 |
1.已知点A(1,3),B(-2,-1),若直线l:y=k(x-3)+2与线段AB没有交点,则k的取值范围是( )
| A. | $k≥\frac{1}{2}$ | B. | $k≤\frac{1}{2}$ | C. | k≥$\frac{3}{5}$或k≤-$\frac{1}{2}$ | D. | -$\frac{1}{2}$≤k≤$\frac{3}{5}$ |