已知双曲线C:$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{{m}^{2}}$=1的左右焦点分别为F1.F2.双曲线外一点P关于点F1.F2的对称点分别为A.B.线段PQ的中点在曲线C上.则|QA|-|QB|的值为( )A．6B．12C．24D．4|m| 题目和参考答案——青夏教育精英家教网——

题目内容

17．已知双曲线C：$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{{m}^{2}}$=1的左右焦点分别为F₁，F₂，双曲线外一点P关于点F₁、F₂的对称点分别为A、B，线段PQ的中点在曲线C上，则|QA|-|QB|的值为（　　）

A．

6

B．

12

C．

24

D．

4|m|

分析利用三角形的中位线的性质，双曲线的定义，即可得出结论．

解答解：设线段PQ的中点为C，则|CF₁|=$\frac{1}{2}$|QA|，|CF₂|=$\frac{1}{2}$|QB|，
∴|QA|-|QB|=2（|CF₁|-|CF₂|）=4a=12，
故选：B．

点评本题考查三角形的中位线的性质，双曲线的定义，考查学生的计算能力，比较基础．

练习册系列答案

精彩考评单元测评卷系列答案

导学案快乐学习系列答案

孟建平各地期末试卷精选系列答案

名师三导学练考系列答案

轻松小卷系列答案

提分百分百检测卷系列答案

权威考卷系列答案

密码大考卷系列答案

宝贝计划期末冲刺夺100分系列答案

能考试全能100分系列答案

相关题目

7．函数$y=\sqrt{{{log}_{\frac{2}{3}}}（2x-1）}$的定义域是（$\frac{1}{2}$，1]．

8．log₃5•log₅6•log₆9=2．

5．在（$\frac{\sqrt{x}}{2}$-$\frac{2}{\sqrt{x}}$）⁶的二项展开式中，x²的系数为-$\frac{3}{8}$．

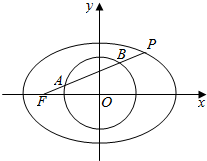如图，过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点F作直线与圆x²+y²=$\frac{{a}^{2}}{4}$及椭圆依次交于点A、B、P，若FA=PB，且AB=$\frac{\sqrt{3}a}{2}$，则椭圆的离心率为$\frac{\sqrt{10}}{4}$．

2．在平面直角坐标系xOy中，将直线l沿x轴正方向平移3个单位，沿y轴正方向平移5个单位，得到直线l₁．再将直线l₁沿x轴正方向平移1个单位，沿y轴负方向平移2个单位，又与直线l重合．则直线l与直线l₁的距离是$\frac{11}{5}$．

9．若复数z满足$|{\begin{array}{l}1&i\\{1-2i}&z\end{array}}|=0$（i为虚数单位），则|z|=$\sqrt{5}$．

如图，有一块平行四边形绿地ABCD，经测量BC=2百米，CD=1百米，∠BCD=120°，拟过线段BC上一点E设计一条直路EF（点F在四边形ABCD的边上，不计路的宽度），将绿地分为面积之比为1：3的左右两部分，分别种植不同的花卉，设EC=x百米，EF=y百米．
（1）当点F与点D重合时，试确定点E的位置；
（2）试求x的值，使路EF的长度y最短．

7．已知A（x₁，y₁），B（x₂，y₂）（x₁＞x₂）是函数f（x）=ln|x|图象上的两个不同点，且在A，B两点处的切线互相垂直，则x₁-x₂的取值范围为（　　）